1.2 Ansätze

1.2.1 Skalen

Eine sehr wichtige Unterscheidung zwischen verschiedenen Maßen betrifft die Art der für den Meßwert verwendeten Skala:

• Nominalskala. Eine Nominalskala ist qualitativ. Als Meßwert wird eines aus einer endlichen Menge von Symbolen verwendet. Zwischen diesen Symbolen ist kein Zusammenhang definiert. Z.B. läßt sich die Programmiersprache, in der ein Programm geschrieben ist, nur auf einer Nominalskala angeben. Bei Nominalskalen spricht man meist nicht von Messen, sondern von Kategorisieren.
• Ordinalskala. Eine Ordinalskala ist ebenfalls qualitativ, jedoch ist auf den Werten eine Totalordnung definiert. Die Antwortmöglichkeiten in Fragebögen haben oftmals diese Art, z.B. ,,zufrieden``, ,,teilweise zufrieden``, ,,unzufrieden``.
• Intervallskala (Differenzskala). Eine Intervallskala ist die schwächste Art einer quantitativen Skala. Sie läßt als einzige Operation auf Meßwerten die Differenzbildung zu. Die Temperatur wird z.B. üblicherweise auf den Intervallskalen Celsius oder Fahrenheit gemessen.
• Verhältnisskala. Auf einer Verhältnisskala hat zusätzlich der Nullpunkt eine ausgezeichnete Bedeutung; man kann dann auch Verhältnisse bilden, z.B.: dieses Programm ist doppelt so lang wie jenes.
• Absolutskala. Der Meßwert gibt eine Anzahl an. Dies ist einerseits ein Spezialfall der Verhältnisskala (denn dort sind evtl. auch gebrochene und negative Meßwerte zulässig), andererseits hat auf einer Absolutskala neben der Null auch die Eins eine ausgezeichnete Bedeutung.

Es ist zu beachten, daß die Skala eine Eigenschaft eines Maßes ist, nicht eine Eigenschaft der zu messenden Größe. So ließe sich die Zufriedenheit auch auf einer Verhältnisskala messen, indem man z.B. den Geldbetrag mißt, den jemand bereit wäre, für den Erhalt eines Zustandes zu bezahlen, den man vermessen möchte. Auch die Temperatur läßt sich auf einer Verhältnisskala angeben: den Kelvingraden.

Die Skala bestimmt, wie oben angedeutet, welche Operationen man auf den Meßwerten sinnhaltigerweise ausführen kann und welche nicht. Demnach sind gewisse Aussagen sinnleer, z.B.:

• Man kann nicht sinnvoll von ,,20 Prozent Verbesserung der Qualität`` sprechen, wenn man nicht festlegen kann, was Qualität Null sein sollte, denn relative Verbesserungen setzen eine Verhältnisskala voraus.
• Wenn jemand sagt, ,,diese Kunden sind doppelt so zufrieden wie jene``, dann hat er wahrscheinlich die 5 Zufriedenheitsstufen eines Fragebogens in die Zahlen 1 bis 5 umkodiert und munter damit herumgerechnet. Der Unsinn tritt zutage, wenn man fragt ,,wie zufrieden sind denn jene``, denn die Antwort würde dann beispielsweise lauten: ,,zwei komma eins``. Das ist reiner Unsinn.

Die meisten Fehler beruhen darauf, daß wir gerne, wenn wir Zahlen sehen, sofort eine Verhältnisskala als gegeben annehmen, etwa bei der Aussage ,,heute ist es doppelt so warm wie gestern``. Das mag bei heute 20 Grad Celsius und gestern 10 Grad Celsius ja gut klingen. Jemand, der die Temperatur in Fahrenheit zu messen gewöhnt ist, würde aber wohl kaum zustimmen, daß 68 Grad Fahrenheit doppelt so warm seien wie 50 Grad Fahrenheit -- das ist aber das Gleiche. Und ein Physiker könnte beide darüber aufklären, daß die Temperatur in Wirklichkeit nur um dreieinhalb Prozent zugenommen hat: von 283 Kelvin auf 293 Kelvin; denn der Nullpunkt der Kelvinskala ist tatsächlich ein Nullpunkt (keine thermische Energie mehr vorhanden).

  
1.2.2 Anforderungen an Maße

Es lassen sich eine Reihe von Anforderungen an Maße formulieren, die erfüllt sein sollten, damit ein Maß nützlich ist. Wie wir unten noch sehen werden, sind leider bisher die Versuche, solche Anforderungen zu formalisieren, weitgehend gescheitert. Deshalb lassen sich nur sehr allgemeine und ungenaue Anforderungen angeben.

• Wohldefiniertheit. Ein Maß sollte eine vollständige und genaue Definition besitzen. Diese Definition muß fehlerfrei zwischen Benutzern des Maßes kommunizierbar sein.
• Aussagekraft. Ein Maß sollte einen Wert ergeben, der Information über eine Größe liefert, welche tatsächlich von Belang für die Softwareentwicklung ist. Das erscheint selbstverständlich, wird aber verblüffend oft mißachtet.
• Sinnhaltigkeit. Diese Werte sollten in ihrer Größe dem Sinn der Messung entsprechen. Dies ist der Kern eines Maßes überhaupt: Wenn die Meßwerte nicht die gemessene Eigenschaft qualitativ gleichartig abbilden, ist das Maß wertlos. Zum Beispiel ist ein Größenmaß sinnlos, das offensichtlich dramatisch unterschiedlich großen Objekten dieselbe Größe zuweist und erst recht ist es sinnlos, wenn es gar dem größeren Objekt in manchen Fällen eine kleinere Größe zuweist. Diese Anforderung enthält insbesondere die Forderung aus der Meßtheorie, die dort Repräsentationsbedingung genannt wird: Die Abbildung von Objekten auf Meßwerte muß die Relationen zwischen den Objekten (im Bezug auf das gemessene Attribut) in dem Sinne erhalten, daß es ihnen entsprechende Relationen zwischen den Meßwerten gibt, die stets gleich ausfallen.
• Genauigkeit. Das Maß sollte hinreichend genau bestimmbar sein, damit Messungen zuverlässig genug sind, um sich auf sie zu verlassen.
• Berechenbarkeit. Die Berechnungsvorschrift für das Maß muß algorithmisch und berechenbar sein.
• Praktische Durchführbarkeit. Die zur Berechnung eines Maßes nötigen Eingabedaten sollten verfügbar sein und zwar zu der Zeit, zu der wir am Meßergebnis interessiert sind.

Dabei müssen wir uns eventuell mit dem Besten zufriedengeben, was wir bekommen können. So sind wir unter Umständen insbesondere bereit, Abstriche bei der Wohldefiniertheit, der Aussagekraft, der Genauigkeit und der Berechenbarkeit zu machen, weil wir entsprechende Maße einfach nicht kennen. Ein Beispiel ist die Zuverlässigkeit von Software. Zu ihrer Bestimmung sind wir meist auf Beobachtungen beim Einsatz der Software angewiesen, die ungenau sind und eigentlich zu spät Ergebnisse liefern. Ein anderes Beispiel ist die Komplexität von Software: Wir kennen kein Maß, das diese zufriedenstellend mißt; also benutzen wir Ersatzmaße, (z.B. das McCabe-Maß, das im wesentlichen die Zahl von binären Abfragen im Programm angibt), deren Aussagekraft eigentlich gering ist.

Zusammenfassend könnte man sagen, die wichtigste Anforderung an ein Maß ist seine Zweckmäßigkeit: In dem Spannungsfeld zwischen wünschenswerten Eigenschaften und durchführbaren Messungen ist die Lösung angebracht, die mir am besten die gewünschte Information liefern kann, also den besten Kompromiß zwischen Kosten und Qualität der Daten darstellt. Wie man solche Maße findet, werden wir kurz in einem getrennten Abschnitt über die Goal/Question/Metric-Methode besprechen (Abschnitt 1.2.4).

1.2.3 Versuch einer Axiomatisierung

Für Maße der Softwarekomplexität gibt es einen Versuch, die wünschenswerten Eigenschaften von Maßen in ein Axiomensystem zu fassen. Dieses System wurde 1988 von Elaine Weyuker vorgestellt [Wey88]. Seien P, Q und R Programmstücke und |P| die Komplexität von P bezüglich eines angenommenen Maßes. Sind zwei Programme syntaktisch identisch, so schreiben wir P = Q, sind sie semantisch identisch, so schreiben wir 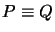$P \equiv Q$. Die textuelle Verkettung zweier Programme notieren wir als P;Q. Die Komplexität sei eine nichtnegative Zahl, so daß sich Komplexitäten totalordnen lassen (im Gegensatz zu Komplexitäten, die durch Vektoren ausgedrückt werden):

1.

$\exists P, Q: \vert P\vert \neq \vert Q\vert$
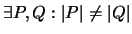
,,Nicht konstant``: Ein Maß darf nicht allen Programmen den gleichen Meßwert zuordnen.

2.

$\forall c \ge 0 : \vert\{P\;\vert\; \vert P\vert = c\}\vert < \infty$
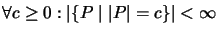
,,Fein genug``: Ein Maß muß die Programme in genügend viele Komplexitätsklassen unterteilen, so daß keine dieser Klassen unendlich viele Elemente hat.

3.

$\exists P, Q: P \neq Q \wedge \vert P\vert = \vert Q\vert$
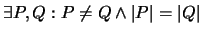
,,Nicht zu fein``: Es gibt Programme, die verschieden sind und dennoch die gleiche Komplexität haben.

4.

$\exists P, Q: P \equiv Q \wedge \vert P\vert \neq \vert Q\vert$
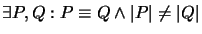
,,Implementationsabhängig``: Zwei Programme können unterschiedliche Komplexität haben, auch wenn sie dieselbe Funktionalität besitzen.

5.

$\forall P, Q: \vert P\vert \le \vert P;Q\vert \wedge \vert Q\vert \le \vert P;Q\vert$
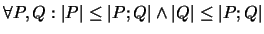
,,Monotonität``: Das Zufügen von Teilen am Anfang oder Ende eines Programms kann seine Komplexität nicht verringern.

6.

a.) $\exists P,Q,R: \vert P\vert = \vert Q\vert \wedge \vert P;R\vert \neq \vert Q;R\vert$
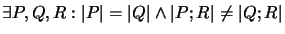
b.) $\exists P,Q,R: \vert P\vert = \vert Q\vert \wedge \vert R;P\vert \neq \vert R;Q\vert$
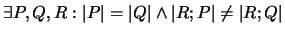
,,Interaktion``: Programmstücke gleicher Komplexität können, wenn man ein identisches Stück anhängt (Fall a), Gesamtprogramme unterschiedlicher Komplexität ergeben. Das gleiche gilt für das Voranstellen (Fall b). Gleich komplexe Programmstücke interagieren also evtl. verschieden mit ihrem Kontext.

7.

$\exists Q,Permutation: P = Permutation(Q) \wedge \vert P\vert \neq \vert Q\vert$
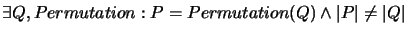
,,Anordnungsabhängigkeit``: Die Komplexität eines Programmstücks kann sich verändern, wenn man die Reihenfolge seiner Anweisungen verändert.

8.

$\forall Q, Renaming: P = Renaming(Q) \Rightarrow \vert P\vert = \vert Q\vert$
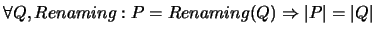
,,Namensunabhängigkeit``: Die Komplexität eines Programmstücks kann sich nicht ändern, wenn man die Programmobjekte umbenennt.

9.

$\exists P,Q: \vert P\vert + \vert Q\vert < \vert P;Q\vert$
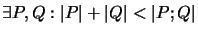
,,Mehr als Summe der Teile``: Diese quasi umgedrehte Dreiecksungleichung besagt, daß ein Programm komplexer sein kann als die Summe seiner Teile.

Zu diesem System von Axiomen sind eine Reihe von Anmerkungen zu machen:

• Die Bedingungen sind nicht hinreichend dafür, daß ein Maß ein gutes Komplexitätsmaß ist. So zeigt [CS91] an einem Beispiel, daß sich willkürliche, sinnlose Maße definieren lassen, die alle Bedingungen erfüllen.
• Die Bedingungen sind aber auch nicht notwendig. Als Beispiel betrachten wir das Maß ,,Datenflußkomplexität``, das für ein Programmstück die Gesamtanzahl von Datenflüssen zu Variablennutzungen angibt, die in irgendeinen Block hineinführen. Dieses Maß ist durchaus nützlich zur Beschreibung der Programmkomplexität, erfüllt aber die Monotonitätsbedingung nicht, weil ein Davorhängen von Anweisungen hereinführende Datenflüsse zu blockinternen Referenzen umwandeln kann.
• Zu beachten ist, daß manche Maße nützlich sein können, obwohl sie keine nützlichen Komplexitätsmaße sind. Beispielsweise verletzt das Lines-of-Code-Maß mehrere der obigen Bedingungen und ist kein gutes Komplexitätsmaß, kann aber dennoch als nützliches Maß betrachtet werden -- nur eben für einen anderen Zweck, nämlich die Beschreibung der Größe.
• Manche der Bedingungen sind skeptisch zu betrachten. So ist z.B. die Forderung nach Namensunabhängigkeit aus psychologischer Sicht sehr dubios. Die Feinheitsforderung (2) ist für viele Zwecke vermutlich übertrieben. Wenn man nur bestimmte Aspekte von Softwarekomplexität betrachtet, können auch noch andere Forderungen unnötig werden; z.B. ist für die Schnittstellenkomplexität der Funktionen in einem Modul die Reihenfolge der Funktionen unerheblich, also Forderung 7 überflüssig.
• Dennoch liefert diese Liste von Anforderungen einen guten Maßstab für den Entwurf oder die Beurteilung von Komplexitätsmaßen. Jede Verletzung einer Anforderung muß gut begründet sein, andernfalls kann man das Maß als unbefriedigend ansehen.

  
1.2.4 Goal, Question, Metric (GQM)

Im vorletzten Abschnitt 1.2.2 haben wir festgestellt, daß die zusammenfassende Anforderung an ein Maß die Zweckmäßigkeit ist. Wie findet man zweckmäßige Maße?

Basili und Weiss haben 1984 eine Methode vorgestellt, mit der man dieses Problem systematisch anpacken kann [BW84]. Sie nennen diese Methode ,,Goal-question-metric paradigm`` oder kurz GQM. Sie besteht aus folgenden Schritten:

1.

Definiere Ziele. Ausgangspunkt jedes Meßvorhabens muß die Frage sein, was man eigentlich erreichen will. Messen ist nicht ein Ziel an sich, sondern dient der Verfolgung gewisser Ziele. Beispiele hierfür könnten sein, die Zahl von ins Programm eingefügter Fehler zu minimieren, die Wartbarkeit der Programme zu verbessern oder die Projektdurchlaufzeiten zu verkürzen. Die Ziele können mehr oder weniger allgemein sein, müssen sich aber jedenfalls direkt an den Geschäftszielen, also an Zwecken, orientieren.

2.

Finde Fragen. Anhand des Messungsziels kann man nun Fragen finden, deren Beantwortung zum Erreichen des Ziels hilfreich wäre. Man konkretisiert das Ziel also in einen Informationswunsch. Zu den obigen Beispielen könnten die Fragen etwa lauten: ,,Was für Fehler machen wir eigentlich? Und wie viele? Wann machen wir sie? Warum machen wir sie¿` oder ,,Welche Programme sind schlecht wartbar? Wie kann man diese frühzeitig erkennen¿` oder ,,Auf welche Arbeiten verwenden wir wieviel Zeit? Welche davon könnte man einsparen? Welche Arbeiten könnte man parallel ausführen¿`.

3.

Definiere Maße. Erst anhand dieser konkreten Informationswünsche sollten nun Maße definiert werden. Das ist in vielen Fällen nach wie vor schwierig, aber zumindest versteht man die Stärken und Schwächen eines Maßes jetzt viel leichter, weil die Fragen einen Maßstab zu ihrer Beurteilung vorgeben. Zu den obigen Beispielen könnten folgende Arten von Messungen sinnvoll sein: Zur Fehleranalyse muß man Fehlerprotokolle führen, die für jeden Fehler eine Fehlerklasse angeben und möglichst den Zeitpunkt, den Arbeitsschritt und die Ursache des Entstehens beschreiben. Zur Wartbarkeitsuntersuchung muß man Hypothesen aufstellen, welche meßbaren Eigenschaften von Programmen (Entwürfe oder Quellcode) die Wartbarkeit beeinflussen und dann dazu Maße aufstellen und ihre Nützlichkeit validieren; wir werden weiter unten einige Beispiele für solche Maße sehen. Solche Maße findet man intuitiv oder mittels induktiver Analyse einiger Programme und deren Wartungshistorie oder mittels schrittweiser Verbesserung vorhandener Maße; die drei Methoden schließen sich natürlich keineswegs aus. Zur Projektbeschleunigung braucht man ein quantitatives Modell des Softwareherstellungsprozesses, das wiederum auf Maßen basiert, die gefunden und validiert werden müssen.

Die Methode von Basili und Weiss beschreibt weiter, wie man das eigentliche Datensammeln auf Basis der nun definierten Maße plant, vorbereitet, durchführt und analysiert, um seine Fragen zu beantworten.

Die wesentliche Nachricht von GQM ist jedoch diese: Bevor Du anfängst irgendetwas zu messen, überleg Dir genau, was Du eigentlich erreichen willst, welche Information Du dazu benötigst und welche Maße Dir diese Information liefern können (oder verwandte Information, die eine genügend gute Annäherung darstellt). Andernfalls sind die Ergebnisse von Messungen keine Information (jedenfalls keine nützliche), sondern nur ein Berg nutzloser Daten. Leider wird dieser elementare Ratschlag in der Praxis oft mißachtet; das Messen und Datensammeln verkommt zum Selbstzweck und richtet aufgrund seiner Kosten und Belästigung mehr Schaden an als es Nutzen bringt.

1.2.5 Auflösung, Genauigkeit und Fehler

Es ist generell beim Messen wichtig, zwischen der Meßauflösung (precision) und der Meßgenauigkeit (accuracy) zu unterscheiden. Die Auflösung beschreibt die Auflösungsstärke des Maßes, also die Anzahl von Maßstufen (für nominale und ordinale Skalen), bzw. den geringsten Unterschied zwischen zwei Meßwerten (für Intervall- und Verhältnisskalen). Zum Beispiel hat eine Messung von Zeitaufwand in Minuten eine höhere Auflösung als eine in Stunden (wenn nur ganze Stunden und ganze Minuten angegeben werden).

Die Genauigkeit hingegen beschreibt, wie weit der gemessene Wert voraussichtlich oder höchstens vom tatsächlichen Wert abweicht, wenn man eine ganze Reihe von Messungen betrachtet. Beispiel: Eine Berechnung des tatsächlichen Gesamtzeitaufwandes in Stunden für ein Projekt könnte man folgendermaßen vornehmen: Für jeden Arbeitstag der Projektdauer multipliziere man die Anzahl der an diesem Tag am Projekt beteiligten Mitarbeiter mit 8. Eine solche Berechnung wäre nicht genauer als etwa 90 Prozent, weil aufgrund diverser Gründe weniger als 8 Stunden pro Tag pro Person für das Projekt gearbeitet werden: manche Mitarbeiter haben auch noch andere Aufgaben, gelegentlich werden Mitarbeiter krank etc. Abhängig von den Umständen könnte es auch eine Abweichung nach oben geben, weil Mitarbeiter viele Überstunden gemacht haben. Eine gute Beschreibung der Genauigkeit erfolgt durch Angabe einer Fehlerverteilung, also einer Wahrscheinlichkeitsverteilung, die die Erwartung über die Größe des Fehlers beschreibt. So könnte in obigem Beispiel idealerweise die Angabe lauten ,,die Ungenauigkeit dieses Maßes ist normalverteilt mit Mittelwert -5 Prozent und Standardabweichung 3 Prozent``, was dann bedeutet, daß in etwa 2.5 Prozent der Fälle eine Abweichung nach unten von mehr als 11 Prozent erwartet wird (denn Abweichungen von mehr als zwei Standardabweichungen haben bei normalverteilten Daten eine Wahrscheinlichkeit von ungefähr 5 Prozent, je zur Hälfte nach oben und nach unten). Häufiger als ganze Wahrscheinlichkeitsverteilungen wird man Angaben von Konfidenzintervallen benutzen, also zum Beispiel ,,in mindestens 95 Prozent der Fälle liegt die Abweichung unter 6 Prozent``.

Der Fehler ist die Ursache von Ungenauigkeit, also die Herkunft der Abweichungen; allerdings werden die Begriffe Fehler und Ungenauigkeit auch oft synonym benutzt. Der Fehler setzt sich zusammen aus dem systematischen Fehler und dem statistischen Fehler. Der systematische Fehler ist eine deterministische (oft sogar konstante) Komponente von Ungenauigkeit, wogegen der statistische Fehler eine Zufallsgröße ist, die jede einzelne Messung gemäß einer gewissen Verteilung stochastisch beeinflußt. Beispiel: Die Messung einer kurzen Zeit mit einer Handstoppuhr hat als systematischen Fehler den regelmäßigen Falschgang der Uhr, beispielsweise plus 0.1 Promille, also ein Vorgehen von 0.36 Sekunden pro Stunde und als statistischen Fehler die zufälligen Schwankungen in der Reaktionszeit des Bedieners, beispielsweise im Mittel plus oder minus 0.05 Sekunden. Im Beispiel überwiegt also bei kurzen Messungen der statistische Fehler, bei langen der systematische Fehler; der Übergang liegt nach etwas mehr als vier Minuten. Ähnliche Betrachtungen sollte man bei jeder gründlichen Genauigkeitsanalyse anstellen.

Die Genauigkeit wird durch die Auflösung beschränkt, jedoch gaukeln hochauflösende Maße oft eine Genauigkeit vor, die in Wirklichkeit gar nicht gegeben ist. Es ist wichtig, die Genauigkeit eines Maßes oder eines einzelnen Meßvorgangs zu kennen oder wenigstens abschätzen zu können und die Genauigkeit bei der Interpretation von Meßergebnissen, insbesondere beim Vergleich mehrerer, immer im Auge zu behalten, weil sonst leicht ungerechtfertigte Schlüsse zustandekommen. Eine gute Abschätzung der Genauigkeit (erst recht in Form einer Wahrscheinlichkeitsverteilung) ist aber häufig sehr schwierig.

1.2.6 Arten von Softwaremaßen

Maße in der Softwaretechnik lassen sich entlang verschiedener Dimensionen unterscheiden, zum Beispiel nach dem Meßgegenstand, nach der Unterscheidung quantitativ/qualitativ, nach der Unterscheidung automatisierbar/teilautomatisierbar/nichtautomatisierbar oder nach der Unterscheidung direkt/indirekt.

Die Unterscheidung nach dem Meßgegenstand ergibt folgende Arten von Maßen:

• Externe Produktmaße. Diese beschreiben Merkmale des Produkts, die von außen sichtbar sind, wenngleich eventuell nur indirekt. Dazu gehören insbesondere Maße für Qualitätsattribute wie die Wartbarkeit, die Zuverlässigkeit, die Benutzbarkeit, die Effizienz etc.
• Interne Produktmaße. Basis für die Charakterisierung externer Produktattribute sind interne Attribute, die sich zumindest zum Teil besser messen lassen. Hierzu gehören z.B. die Größe, die Modularität und die Komplexität.
• Prozeßmaße. Diese charakterisieren Eigenschaften des Produktionsprozesses, z.B. die typische Produktivität, Kostenaufteilung auf bestimmte Arbeiten, Dauer von Arbeitsschritten etc.
• Ressourcenmaße. Diese charakterisieren Eigenschaften der im Prozeß verwendeten Ressourcen, z.B. die Auslastung von Rechnern, die typische Produktivität und Fehlerrate eines bestimmten Ingenieurs etc.

Wir werden diese Kategorien in nachfolgenden Abschnitten noch genauer besprechen.

Quantitative Maße sind solche, deren Meßwerte Zahlen sind und das Rechnen mit ihnen erlauben (also Maße mit Intervallskala oder höheren); alle übrigen Maße sind qualitativ. Ein Beispiel für ein qualitatives Maß ist das ,,Strukturierungsniveau`` eines Programms, das auf einer Ordinalskala mit den Stufen mitGoto, strukturiert, modularisiert, objekt-orientiert gemessen werden könnte. Es ist wichtig, sich darüber klar zu sein, daß aus dieser Ordinalskala auch dann keine Differenz- oder gar Kardinalskala wird, wenn man diesen Stufen jetzt z.B. die Werte 0, 1, 2, 3 zuweist. Rechenoperationen mit diesen Werten wären irreführend und weitgehend sinnlos.

Maße sind automatisierbar, wenn ich sie in einem Computerprogramm formulieren kann und alle Eingabedaten zur Verfügung stehen. Sie sind nicht automatisierbar, wenn Entscheidungen von Menschen getroffen werden müssen z.B. Zuweisung einer Fehlerart.

Wir nennen ein Maß direkt, wenn es unmittelbar durch einen einzelnen Meßvorgang ermittelt wird, wie z.B. Lines of Code oder Gesamtanzahl Fehler. Die meisten Maße sind jedoch indirekt, d.h. sie basieren auf mehreren Meßvorgängen, deren Ergebnisse durch Rechnung verbunden werden, z.B. Fehlerdichte als Gesamtanzahl Fehler geteilt durch Lines of Code.