Next: 6 Critical Points and Up: Visualizing Data from Time-Dependent Previous: 4 A Framework for
Next: 6 Critical Points and Up:
Visualizing Data from Time-Dependent Previous:
4 A Framework for
On adaptive meshes with changing
discretization, care has to be taken when using integration schemes. Let us now
focus on several important aspects. Schemes like the Runge-Kutta or the
Euler-Cauchy scheme are frequently used for particle tracing and related methods
[34][23]. Assuming
smoothness of the data, they are of second or higher order with a consistency
error of third order. But in most finite element and finite volume strategies in
CFD, the resulting velocity field is at most 
, or even discontinuous
at the boundary faces of the elements; only in the interior of an element is the
solution smooth. These features stand out in areas of rapidly changing data,
such as shocks in the physical solution, especially if they have been resolved
by the CFD algorithm by intensive local refinement. It's difficult to handle
them with a standard scheme. Note that even a step size control based on
information about the extracted path does not necessarily take accurate account
of discontinuities in the data. The following modified Euler-Cauchy scheme for a
single integration step overcomes this problem. It first shortens the
integration step size 
such that the time when the discretization changes again
won't be crossed. Then it correctly picks up all element boundaries in space:
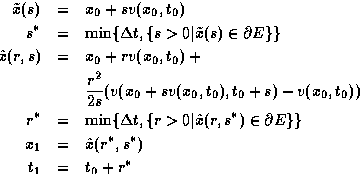
Here 
is the particle position at time 
in an element 
, 
the
velocity in the current element at a position 
and at time 
, and 
is the
particle position at time 
. At a boundary face the algorithm switches from one
element to the adjacent element. A direct but tedious calculation proves that
this scheme is consistent of the order 
where 
is the
local grid size, and that it integrates fields of piecewise linear velocity
accurately. Let us remark, that the case where the velocities in two adjacent
elements are of opposite common direction needs some extra effort.
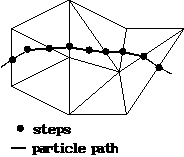
Furthermore, it is useful to keep track not only of the world coordinates but
also of the pair 
of element and local coordinates for each particle
position. As already mentioned in section 3,
this is essential for an efficient evaluation of the numerical velocity field.
Passing the boundary face of an element on a fixed mesh, as it occurs in the
above scheme, implies a simple shift in the coordinate vector. But each change
of the discretization entails a search for the right element and local
coordinates on the new mesh. The following rules guarantee that this can still
be done efficiently:
on the new mesh and keep track of the elements
passed along a line to the current position . relative to the
old mesh. If the local adaption area is not met the new pair
will in general coincide with the old one.
of some point in the set. Take this for a guess at the position of its
neighbouring points. Having found them, go on recursively.
Next: 6 Critical Points and Up:
Visualizing Data from Time-Dependent Previous:
4 A Framework for