For large, nonlinear, and time dependent PDE constrained optimization problems with 3D spatial domain, reduced methods are a viable algorithmic approach. The computation of reduced gradients by adjoint methods requires the storage of 4D data, which can be quite expensive from both a capacity and bandwith point of view. This project investigates lossy compression schemes for storing the state trajectory, based on hierarchical interpolation in adaptively refined meshes as a general predictor.
The goal of this project to speed up the computation of curvature flows, previously implemented on the CPU. This project will in particular demonstrate numerics that fully utilize the SIMT (single-instruction, multiple-thread) architecture of modern Graphics cards (GPU), and provide a proof-of-concept implementation of advanced geometry processing on the GPU. In particular, industrial design and CAD companies could use such fast curvature flow or smoothing algorithms for their laser scanners to quickly capture models accurately and cheaply compared to their current setup.
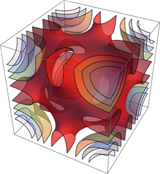
A discrete implicit surface is considered as the zero set of a scalar-valued function on an ambient 3-dimensional simplicial complex. In contrast to the discrete geometry of simplicial surfaces, the differential operators of implicit surfaces live on the ambient grid. The purpose of this project is to derive a discrete differential geometric toolbox for implicit surfaces similar to (explicit) discrete surfaces. This includes the development of discrete differential operators for implicit surfaces including curvature operators, and the study of curvature flows. A major application is the computation of (parametric) discrete minimal surfaces whose topology is a priori unknown.
Surface meshes often appear in a quality and resolution which is unsuitable for many geometry processing algorithms. This project aims at the automatic improvement of surface meshes.
- Study of hierarchical surface meshes
- Generation of nested mesh hierachies
- Computation of chart parameterizations
We develop new algorithms and study prototype implementations.
The long term goal of the Uplivion project is to replace the DVD as the primary means of distributing high-end computer games and to make them available through the web browser instead. Our technology enables players to start playing a game by simply navigating to a website and pressing the play-button, much in the same way as watching a video on YouTube.
To make this possible, we are developing a highly optimized suite of technologies that cover all aspects of streaming games across the internet.
Our project has been awarded the EXIST-grant and started in March 2011.
Laubwerk, founded in April 2010 and supported by an EXIST-grant, enables for the first time architects and landscape architects to get the full variety of plant life on their computer.
The Laubwerk team developed a novel technology in combination with a skeleton-based storage format and a software library to flexibly build geometries for 3D plant models. This allows the user to fluently work with 3D plants in a preview mode and guarantees high-end visualization in a breathtaking quality and performance.
Mathematics is everywhere: in mobile phones, MP3 players, and computers, just to name a few; it is a fundament of science and technology. Still its reputation could be better: it is usually regarded as an abstract subject, tedious and too dry to be comprehensible, with its uses often remaining often a mystery.
vismath, founded in March 2010 and supported by an EXIST-grant, aims at a change: presenting mathematics in an inspiring and vivid way, accessible for everyone and unveiling its effective applications in today’s world.
Surface meshes obtained from a 3D laser-scanner typically include high-frequency noise and distortions due to scanning inaccuracies. Special discrete variants of anisotropic mean curvature flows have proven to remedy noise artifacts while maintaining or even improving quality of the surface mesh. Industrial surface models typically have a large number of variable nodes leading to long running times. This project will investigate to accelerate the compute time by using the latest Cuda library. Cuda allows to drastically reduce the compute time by shifting computing resources from the main processor to the highly parallel graphics card. The project investigates the underlying differential geometry of mean curvature flow, its discretization and its efficient implementation on a Cuda graphics card.
The project was part of Research in Industrial Projects for Students (RIPS) 2010 program organized by the Institute for Pure and Applied Mathematics (IPAM) and Matheon.
The project develops visualizations and didactic concepts for teaching mathematical algorithms in schools. Understanding how an algorithm works is crucial and often accomplished best by simulating it in some way. Computers provide the means to make these simulations efficient and fun, compared to classical pen-and-paper approaches.
This is another project within the DFG Research Center MATHEON - "Mathematics for key technologies". The main goal of this project is the discretization of classical differential geometry: to find proper discrete analogs of differential geometric objects, notions, and methods, and to develop a corresponding theory. Such a discrete differential geometry has applications in computer graphics, numerics, and visualization.
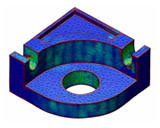
Topology optimization solves the problem of optimally distributing a given amount of material in a given design space subject to load and support conditions. An important application is the design of stable and lightweight mechanical parts.
In manufacturing, sheet metal is a preferred material. Therefore, a desired goal is to incorporate the information obtained by topology optimization into the design of parts made of sheet metal.
We identify planar regions in an optimal distribution of material and provide supporting tools for translating the essential structure of optimal mechanical parts to sheet metal parts.
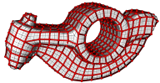
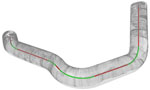
Laser range scanners allow highly accurate measurement of manufaturing parts such as tubes. However, generic surface reconstruction software does not give the specific information needed for quality assurance and cannot provide correction data for the tube bending process. Our aim is to find a tubular geometry which fits best with the measured data.
- Segmentation of point cloud data
- Parametric registration of geometric primitives
- Real-time processing of sampling data
We provide methods for accurate reconstruction of tubular sufaces and provide relevant information for quality assurance and reverse engineering.
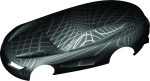
Class-A denotes the highest quality standard for industrial surfaces such as a car body. The characterization and computation of Class-A surface involve serious mathematical challenges:
- Mathematical characterization of Class-A surfaces.
- Non-linear energy functionals and error bounds based on geometric properties.
- Real-time optimization methods for CAD modeling processes.
We offer software solutions for mesh optimization - preserving non-linear features and providing noise removal for industrial 3D meshes.
Numerical simulations and the rendering of complex virtual scenes
is often limited by the huge size of the involved geometry meshes.
This project researches the geometric and topological properties
of mesh representations to solve the following challenges:
- An efficient and redundant-free representation of 3D geometry meshes.
- Fast online transfer of 3D data sets.
- Toolbox for rapid compression and decompression.
We develop algorithms and implementations for mesh compression, including surface attributes like textures and normals.
This project is a university cooperation between the mathematics institutes of FU Berlin with mathematics institutes at the University of Belgrade, the Mathematics institute of SANU (Serbian Academy of Sciences), the faculties of Sciences and Mathematics, Mechanical Engineering and Electronical Engineering at the University of Nis, the department of Mathematics at the University of Sofia and the department of geometry at the University of Technology and Economics in Budapest, the faculty of Electrical Engineering and Information Technology of Ss. Cyril and Methodius University of Skopje, the faculty of Civil Engineering of the University of Zagreb, and Fachinformationszentrum Karlsruhe. "Multimedia Technology for Mathematics and Computer Science Education" is a project within the DAAD-Sonderprogramm "Akademischer Neuaufbau Südosteuropa".
This project splits into two parts: Mathematical Visualization and web based software on the hand, and Electronic Information and Communication on the other. The goal is the development of multimedia courseware and the establishment of a cooperative networks for enhanced knowledge transfer. "Development of Electronic Information Infrastructure and Multimedia Courseware" is a project within the DAAD-Sonderprogramm "Akademischer Neuaufbau Südosteuropa".