Some new Surfaces
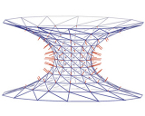
This catenoid is a complete discrete minimal surface whose vertices are
given by explicit formulas.
This surface belongs to a 4-parameter family of complete discrete
catenoids from which a 2-parameter subfamily interpolates the smooth
catenoid. The discrete catenoids are the first explicitly known discrete
versions of a complete minimal surface beside the trivial plane which are
critical points of the variational problem for minimizing the discrete
surface area. This explicit representation allows to generate exact discrete
minimal surfaces without numerical errors which is useful, for example, in
stability investigations.
Discrete H-T Surface (K.
Polthier, 2002)
preprint
preprint
The discrete H-T surface is a triply periodic minimal surface solving a
free boundary value problem for the surface area. This example is of high
numerical precision, and including its parametrization it was automatically
computed by minimizing the alignment energy of a non-conforming conjugate
minimal surface.
Minimizing the alignment energy in the space of non-conforming meshes
enables us to produce discrete conforming minimal surfaces of a high
numerical precision. The computed discrete H-T surface is a non-trivial
example in the sense that it includes a branch point which is not induced
from symmetry properties.
Discrete Schwarz P-Surface (K.
Polthier, 2002)
preprint, compare with http://www.eg-models.de/2001.01.047
preprint, compare with http://www.eg-models.de/2001.01.047
This discrete version of Schwarz' P-surface is a critical point of the
area functional in the space of non-conforming meshes solving a free
boundary problem.
Non-conforming meshes are a superset of the class of conforming meshes
which appear as natural completion in the study of discrete constant mean
curvature surfaces. For example, there exists a 1-1 pairing of discrete
conforming and discrete non-conforming minimal surfaces.
Penta is a compact H-surface of genus 5 with pentagonal symmetry and is
the first compact H-surface of genus > 1 which is successfully computed with
a computer. The surface is defined via the conjugate surface construction by
a two-parameter problem of minimal surfaces in S3. Numerical
existence was shown by computing a sequence of H-surfaces with the algorithm
of Oberknapp/Polthier and using a winding number argument. Further details
on the Penta surface and its cousin are given in the
article section.
Lawson Surface with CMC Surface
(B. Oberknapp, K. Polthier, 1996)
preprint
preprint
Blaine Lawson found in 1970 a method to solve free boundary value
problems for unstable Euclidean constant mean curvature surfaces by solving
a corresponding Plateau problem for minimal surfaces in S3.
Numerical simulations of this construction using standard numerical methods
have failed up to now. The authors have found a
numerical algorithm for this so-called
"Conjugate Surface Construction for H-surfaces" based on the concept of
discrete constant mean curvature surfaces. For the first time it allows
computation and numerical experiments of a large set of H-surfaces, see e.g.
the Penta surface in this image collection. The algorithm is implemented in
the mathematical visualization software
Grape.
The front object in the current picture shows a compact minimal surface
of Lawson in S3 after stereographic projection from S3
to R3 (it looks smooth but the surface is 'discrete' at a fine
level) and the object in the background is its conjugate surface, a periodic
H=1 surface in R3.
Quadend (H. Karcher, K. Polthier,
1995)
preprint
preprint
The Quadend surface is a candidate for a family of a periodic minimal
surfaces, where the genus of the fundamental building block can be made
arbitrarily large. It is not yet completely proved but it is likely that the
period problem can be made independent of the genus.
Hyperbolic Scherk Surface (K.
Polthier, 1993)
preprint
preprint
This surface belongs to a collection of new minimal surfaces in
hyperbolic 3-space which I constructed in my
thesis. These surfaces are solutions to a general Plateau Problem in H3
where parts of the boundary may lie in infinity and some other parts in the
finite space.
The hyperbolic Scherk surface is an example which generalizes in some
sense the Euclidean minimal Scherk surface which is given as a minimal graph
over the white fields of a checker board. Here a major difference between
minimal surfaces in Euclidean and hyperbolic space can be seen: the
Euclidean surface is isolated with respect to its flat ends but the
hyperbolic Scherk surface belongs to a family whose fundamental domains have
the same finite boundary but different infinite boundaries. With other
words, the conformal structure has much more freedom for a given finite part
of a Plateau Problem.