3.5 Beispiel: N-Versions-Programmierung

In diesem Abschnitt besprechen wir ein Beispiel für vorbildliche experimentelle Arbeit im Bereich des Software-Engineering. Das vorliegende Experiment von John Knight und Nancy Leveson [KL86] ist hervorragend entworfen, sauber durchgeführt und ausgewertet und leistet einen wichtigen wissenschaftlichen Beitrag.

3.5.1 Forschungsfrage

Die Ausgangsfrage war, ob eine Annahme, die bei der N-Versions-Programmierung gemacht wird zutrifft oder nicht. Als N-Versions-Programmierung bezeichnet man die Methode, mehrere Programme zu erstellen (zum Beispiel drei oder fünf), die dasselbe berechnen, und im Betrieb dann die endgültige Ausgabe mit einem Abstimmungsverfahren aus den Ausgaben der Einzelprogramme zu ermitteln. Hat eines der Programme bei der vorliegenden Berechnung einen Fehler gemacht, so wird es bei der Abstimmung von den anderen überstimmt und der Fehler richtet keinen Schaden an. N-Versions-Programmierung erhöht also die Zuverlässigkeit des Gesamtsystems, vorausgesetzt, es machen nicht alle Programme stets bei den gleichen Berechnungen Fehler. Bei der N-Versions-Programmierung wird sogar vom entgegengesetzten Verhalten ausgegangen: Die Versagen aller Programme sind statistisch voneinander unabhängig. Für diesen Fall ergibt sich bei einer Versagenshäufigkeit jedes Einzelprogramms von p eine Häufigkeit des Versagens von zwei Programmen gleichzeitig von p² usw. Um dies zu erreichen, fordert die N-Versions-Programmierung eine sehr sorgfältige Problembeschreibung, die frei von Mehrdeutigkeiten und Widersprüchen ist, und eine Implementation durch voneinander unabhängige Entwicklungsteams, die möglichst verschiedene Herangehensweisen benutzen sollen. Diese Vorgehensweise, so die Annahme der N-Versions-Programmierung, führt dann dazu, daß die Versionen nur verschiedene Fehler enthalten (wenn überhaupt welche) und die Versagen dieser Versionen im Betrieb voneinander statistisch unabhängig sind. Die Annahme dieser Unabhängigkeit wurde im vorliegenden Experiment geprüft. Sind die Versagen nicht statistisch unabhängig, so steigt die Zuverlässigkeit eines N-Versions-Programms gegenüber einem einzelnen Programm weniger stark an als erwartet, und die Benutzung der Annahme würde uns in trügerische Sicherheit wiegen.

Dieser Forschungsfrage liegt die Vermutung zugrunde, daß gewisse Teile eines Problems inhärent schwieriger sind als andere und daß deshalb verschiedene Programmierer, selbst wenn sie eine unterschiedliche Ausbildung haben und verschiedene Methoden benutzen, tendenziell die gleichen Fehler machen.

3.5.2 Experimentidee

Die Grundidee des vorliegenden Experiments besteht darin, eine große Anzahl von Versionen eines Programms für dasselbe Problem unabhängig voneinander schreiben zu lassen und dann anhand einer großen Zahl zufällig erzeugter realistischer Testfälle zu prüfen, ob gemeinsames Versagen von zwei oder mehr Versionen häufiger vorkommt, als bei Unabhängigkeit zu erwarten wäre, oder nicht.

3.5.3 Experimentaufbau

15 ,,undergraduate`` Studenten, 8 ,,graduate`` Studenten und 4 Doktoranden schrieben 27 Versionen eines Programms in Pascal. Alle hatten eine ausreichende Ausbildung in Informatik und Mathematik und gute Pascal-Kenntnisse. Sie investierten pro Version im Mittel 5 Stunden zum Verstehen der Aufgabe, 16 Stunden zur Implementation und 27 Stunden zum Test; die resultierenden Programme waren zwischen 327 und 1004 Zeilen lang. 18 der Studenten waren von der University of California in Irvine, 9 von der University of Virginia. Dies erlaubt zu prüfen, inwieweit gleiche Ausbildung eine Rolle spielt. Die Versuchspersonen wurden instruiert, nicht über die Aufgabe oder ihre Lösungsansätze miteinander zu diskutieren, um eine unabhängige Bearbeitung der Programme sicherzustellen.

Die Aufgabe bestand darin, aus einem Eingabevektor von Radarreflektionen anhand einer vorgegebenen Menge von Bedingungen zu ermitteln, ob diese Reflektionen von einer anfliegenden Rakete stammen oder nicht. Die Anforderungsbeschreibung zu dieser Aufgabe war sehr sorgfältig aufbereitet und auf Klarheit und Eindeutigkeit geprüft. Sie war schon in früheren Studien verwendet worden, aus denen auch ein äußerst sorgfältig getestetes Programm, das sogenannte Gold-Programm, vorlag, das als fehlerfrei angenommen werden kann und als zusätzlicher Vergleichsmaßstab in der detaillierten Fehleranalyse eingesetzt wurde. Zur Lösung der Aufgabe waren mathematische Kenntnisse erforderlich (Winkelberechnungen) und ein sorgfältiger Umgang mit Genauigkeitsproblemen in den (Fließkomma)berechnungen.

Außer der boolschen Ausgabe hatten die Programme gemäß Anforderungsbeschreibung eine $15 \times 15$boolsche Matrix und einen 15elementigen boolschen Vektor als Zwischenergebnisse abzuliefern, die die einzelnen Bedingungen repräsentieren, insgesamt also 241 Bits. Als Versagen wurde bereits gewertet, wenn zwei Programme in irgendeinem dieser Bits nicht übereinstimmten.

Jede Versuchsperson erhielt zum Testen 15 Sätze von Eingabe- und zugehörigen Ausgabewerten. Bevor ein Programm als eine der 27 Versionen akzeptiert wurde, wurde es einem Abnahmetest mit 200 zufällig ausgewählten Fällen unterworfen und zurückgewiesen, wenn dabei irgendein Fehler auftrat. Die Zufälligkeit der Testfälle sollte hier dafür sorgen, daß nicht Programme mit gleichen Fehlern (die bei einer bestimmten festen Menge von Testfällen gerade nicht zum Vorschein kommen) selektiv den Abnahmetest passieren konnten. Diese Prozedur entspricht bei wirklicher Anwendung von N-Versions-Programmierung einem gründlichen Test jeder unabhängig entwickelten Version vor ihrer Auslieferung.

Die akzeptierten Versionen wurden schließlich einem extensiven Test unterworfen, der eine Million Fälle umfaßte. Diese Anzahl repräsentiert die gesamte Lebensdauer des N-Versions-Programms. Die Eingaben wurden (wie auch die übrigen in diesem Experiment) von einem speziell für dieses Problem entwickelten Testdatengenerator erzeugt.

Folgendes mathematische Modell wurde zur Prüfung der Unabhängigkeit verwendet. Sei für die N Versionen 1 bis N die Versagenswahrscheinlichkeit der Version i gleich p_i und seien diese Versagen unabhängig voneinander. Dann ist die Wahrscheinlichkeit P₀ dafür, daß auf einem zufällig gewählten Testfall keine einzige der Versionen versagt

$$P_0 = \prod_{i=1}^N 1-p_i$$

und die Wahrscheinlichkeit P₁, daß genau eine versagt ist

$$P_1 = \sum_{i=1}^N p_i \frac{P_0}{1-p_i}$$

damit ergibt sich für jeden Testfall die Wahrscheinlichkeit P_m, daß zwei oder mehr Versionen zugleich versagen als

P_m = 1 - P₀ - P₁

Betrachten wir nun die Gesamtheit aller n Testfälle. Sei K die Zahl von Testfällen, auf denen zwei oder mehr Versionen versagen. Diese Größe ist binomialverteilt. Bei unabhängigem Versagen ist dann die Wahrscheinlichkeit dafür, daß K den Wert x hat, gleich

$$P(K=x) = {n \choose x} P_m^x\cdot (1-P_m)^{n-x}$$

Dies ist also die diskrete Dichtefunktion für K. Für große Werte von n nähert sich eine solche Binomialverteilung einer Normalverteilung. Deren Mittelwert ist dann $n\,P_m$ und die Varianz beträgt $n\,P_m (1-P_m)$. Im vorliegenden Fall ist n sehr groß, deshalb benutzen wir anstelle von K die entsprechende standardnormalverteilte Größe z.

$$z = \frac{K - n\,P_m}{\sqrt{n\,P_m (1-P_m)}}$$

Die Nullhypothese des Experiments lautet mit diesem Ansatz, daß zein korrektes Modell für K ist, wenn P_m aus den Beobachtungen geschätzt wird.

3.5.4 Ergebnis

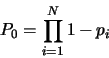
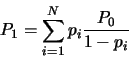
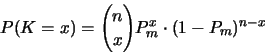
Alle 27 Versionen waren zuverlässiger als 99 Prozent, 23 sogar zuverlässiger als 99.9 Prozent, 6 funktionierten ganz fehlerfrei. Die Versionen waren also nicht weniger zuverlässig, als man das von professionell entwickelten Programmen erwarten kann.

In 1255 der 1000000 Testfälle trat ein Versagen in mehr als einer Version auf. Zusammen mit dem aus den Versagenshäufigkeiten der einzelnen Versionen berechneten Wert für P_m ergibt sich daraus ein Wert für z von 100.51. Die Wahrscheinlichkeit, einen solchen Wert für eine standardnormalverteilte Größe zu erhalten, ist kleiner als ein Milliardstel. Die Hypothese, daß z die Daten modelliert, wird deshalb zurückgewiesen und somit ebenso die Annahme, daß die Versagen der Versionen voneinander unabhängig seien.

Knight und Leveson ziehen die folgenden Schlüsse:

1.

Die Annahme der Unabhängigkeit von Versagen in N Versionen eines Programms wird zurückgewiesen mit einer Konfidenz von 99 Prozent. (Tatsächlich sogar wesentlich höher.)

2.

Dieses Ergebnis gilt für die im Experiment betrachtete Anwendung. Es ist unbekannt, ob sich das Ergebnis auf andere Anwendungen übertragen läßt.

3.

Jedenfalls darf aber die Annahme von Unabhängigkeit nicht mehr ohne weiteres verwendet werden.

4.

Das bedeutet nicht, daß N-Versions-Programmierung nicht nützlich ist. Jedoch muß die Modellierung der Zuverlässigkeit verbessert werden.

5.

Weitere Forschung ist nötig, um die Ursachen zu bestimmen, aus denen gemeinsame Fehler in Programmen hervorgehen oder verwandte Fehler, die gemeinsame Versagen produzieren.

3.5.5 Diskussion

Diese Arbeit ist wie gesagt ein vorbildliches Beispiel für experimentelles Vorgehen aus folgenden Gründen:

• Gute Auswahl der Forschungsfrage: Die untersuchte Fragestellung ist einerseits so bedeutsam, daß das Ergebnis sehr relevant ist, und zugleich so eng, daß eine sorgfältige und erfolgreiche Bearbeitung möglich bleibt.
• Guter Experimententwurf: Die Autoren haben sorgfältig darauf geachtet, einen Aufbau und eine Durchführung zu erhalten, die Zweifel an der internen Gültigkeit des Experiments möglichst ausräumt. Von der Auswahl der Programmieraufgabe, über die Wahl der Versuchspersonen, bis hin zur Durchführung der Implementationen werden die für N-Versions-Programmierung geforderten Rahmenbedingungen eingehalten. Die Auswertung ist so gründlich, daß die Richtigkeit der Beobachtungen außer Frage steht, der Umfang der Tests so groß, daß eine Zufälligkeit ausgeschlossen werden kann.
• Gute Argumentation: Knight und Leveson argumentieren auch geschickt, um eine hohe externe Gültigkeit ihrer Beobachtungen zu bezeugen. Kritik an der Verwendung studentischer anstatt professioneller Programmierer wird dadurch widerlegt, daß die Zuverlässigkeit der einzelnen Versionen auf professionellem Niveau liegt. Die relativ geringe Größe der Arbeit wird deshalb als unschädlich eingestuft, weil auch in größeren Systemen die N-Versions-Programmierung aufgrund ihrer hohen Kosten meist nur für recht kleine Einzelteile eingesetzt werden kann.
• Gute Aufbereitung: Die Forschungsarbeit wird verständlich dargestellt, sowohl von ihrer Idee, als auch von ihrem Aufbau und ihren Ergebnissen. Es gibt eine gründliche Einführung und übersichtliche Information auch über Details. Mögliche Kritikpunkte werden ausdrücklich angesprochen und diskutiert.
• Vorsichtige Auslegung der Ergebnisse: Knight und Leveson ziehen nur äußerst vorsichtige Schlüsse aus ihren Ergebnissen und sind auch beim Aufzeigen der Konsequenzen sehr bedächtig. So nennen sie nur eine Konfidenz von 99 Prozent, obwohl die Daten wesentlich mehr hergeben, erheben nicht den Anspruch, das Ergebnis zwangsläufig auf andere Probleme übertragen zu können und sprechen der N-Versions-Programmierung auch nicht die Daseinsberechtigung ab.

Es sei hier angemerkt, daß die Arbeit aber auch durchaus nicht perfekt ist. Zum Beispiel ist nirgends erwähnt, wie viele Versionen im Abnahmetest versagt haben und wie oft, was daraufhin jeweils geschah und wie wir das in Bezug auf die Ergebnisse vielleicht zu interpretieren haben.

Aber dennoch: Angesichts dieser Qualitäten stimmt es nachdenklich, wie sehr Knight und Leveson von einigen Befürwortern der N-Versions-Programmierung für ihre Arbeit angegriffen wurden. Diese Angriffe waren so heftig, daß Knight und Leveson sich mehr als 4 Jahre nach dem Erscheinen des Artikels genötigt sahen, eine öffentliche Antwort auf die Kritik zu schreiben, die 1990 in den Software Engineering Notes erschien [KL90]. Diese Antwort ist eine furiose Entkräftung der Angriffe, die zum Teil an der Sache vorbeigingen und zum Teil sogar unwahre Behauptungen über den Aufbau des Experiments oder seine Ergebnisse aufstellten. Ich empfehle jedem, sich diesen Artikel zu Gemüte zu führen; es ist ein Genuß, ihn zu lesen.