|
|
Touching Soap Films |
|
|
|
The Method of Weierstraß
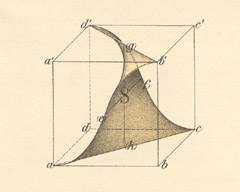
The work of Robert Osserman of Stanford University (California) in the early 1960s ushered in developments that led to the construction of new unbounded minimal surfaces. Osserman's work revived a method of Karl Theodor Weierstraß (1815-1897), who was active in Berlin. Long before the aforementioned calculus of variations could be applied to minimal surfaces, it had been observed that there is a close connection between minimal surfaces and another great direction in mathematics: complex analysis, which was already flourishing in the 19th century, and which was concerned with the properties of complex numbers and functions. Using complex analysis, Weierstraß discovered his "representation formulas" which describe any minimal surface. Inserting an arbitrary pair of two complex functions into the Weierstraß formulas provides for the mathematical representation of a minimal surface. But, it is hard to conclude the geometric shape of the resulting surface, e.g. whether or not surfaces obtained in this way will intersect themselves. Hence this approach is satisfactory only for the description of a small portion of a surface, but it is still invaluable for mathematical theory. A group around the German mathematician Hermann Amandus Schwarz (1843-1921) succeeded in 1865 in finding, for special boundary curves, functions (more exactly, differential forms) that - when inserted into the representation formulas - provide the solution for the Plateau problem for this boundary curve (cf Fig 6). However, after Douglas and Rado had accomplished their breakthrough in 1931 with the help of the calculus of variations, the methods of Weierstraß and Schwarz retreated farther into the background. Their present success comes from the fact that, based on the work of Osserman, the shape of many minimal surfaces can be controlled out to infinity. |