|
|
Touching Soap Films |
|
|
|
Triply Periodic Minimal Surfaces
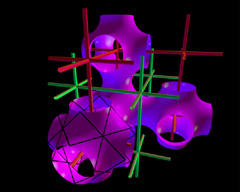
We turn now to a special class of minimal surfaces for which techniques for alteration are well developed, and which have generated great interest in neighboring sciences. We are speaking of surfaces, like the Schwarz P-surface illustrated in Fig 5 and Fig 13, which make a certain kind of three-dimensional structure. Such a structure-a so-called crystallographic cell-is constructed so that using it as a building block one can fill three-dimensional space with no gaps. By analogy with the situation in the plane, one speaks of a tiling of space. Besides the square prism (and a number of other shapes), suitable shapes for such a tiling include prisms whose base is either an equilateral triangle or a regular hexagon. Here we are not preferentially interested in reflection in edges, but rather in reflections in the traditional sense in suitable face planes of the building blocks, which have the same symmetry as the entire tiling. Triply periodic minimal surfaces have-in the simplest cases, which we want to examine here-the same symmetry as that of a crystallographic tiling. In this context, interest lies almost exclusively in embedded surfaces. In particular these surfaces play a role in the description of molecular partitioning in crystals and in the separation surface between the components of a polymer, since they partition space in a natural way into two interpenetrating labyrinths. We call the piece of a triply periodic minimal surface that lies inside a crystallographic cell a fundamental module or simply a cell. The fundamental module is therefore cut out of the triply periodic minimal surface by the face planes of the crystallographic cell. The boundary curves of this cut-out fundamental module consist of lines of symmetry on the face planes and possibly also edges of the crystallographic cell. The simplest example of such a surface was already known to Schwarz (Fig 5, Fig 13). Its fundamental module intersects the faces of a cube in almost circular lines of symmetry. All of the reflection symmetries of a tiling of space by cubes are therefore symmetries of the surface. The fact that there are also straight lines in the surface especially interested Schwarz-with good reason, as we shall see. A reflection in one of the midplanes of the cube, followed by a reflection in one of the sides parallel to this plane, is equivalent to a displacement along one of the edges of the cube. One can therefore regard the complete surface as generated by a sequence of such displacements. The midpoints of the cube can be joined by tubes that do not touch the surface (red in Fig 13), while the connected tubes on the other side of the surface (green in Fig 13) are equal to the edges of the original cubes. If one thinks of these red and green lattices as skeletons, on which flesh grows until they fill all of space, one can obtain an intuitive understanding of how the minimal surfaces partition space into two interpenetrating labyrinths. Alan Schoen, now at Southern Illinois University at Carbondale, has christened these lattice scaffolds as skeletal graphs of the labyrinths. By reflection in the straight lines of the Schwarz surfaces, the inside and outside labyrinths are exchanged, and therefore they both have the same shape. In 1970 Alan Schoen used the idea that minimal surfaces are equilibrium separating surfaces between skeletal graphs in order to supplement the set of five triply periodic minimal surfaces known to Schwarz's school by finding twelve additional complicated examples. Since the existence of complete minimal surfaces, as described above, can be lost as a result of slight deformations, mathematicians were unable to accept Schoen's arguments as existence proofs. However, he confirmed his arguments in the laboratories of NASA by measurements on soap films, like Plateau in the preceding century. He also constructed plastic models according to these measurements, and these models attracted great interest among crystallographers. |