|
|
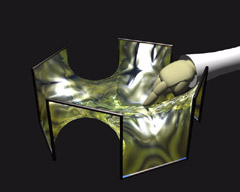
Touching Soap Films |
|
|
|
Plateau Problem
The exact description of minimal surfaces has been the aim of two centuries of mathematical research up to our time. In recent years this field has enjoyed a lively renaissance with the help of modern visualization techniques. To find an optimum (such as to find a minimal surface) belongs to the central problems in many areas of life. Every day we are trying to find the shortest distance or finish projects in the least amount of time. In 1760 the versatile mathematician Joseph-Louis de Lagrange (1736-1813), Professor at Turin, Berlin, and Paris, recognized that the problem of area minimizing is a characteristic model problem for many practical phenomena and that a detailed study of its properties would lead to far-reaching insight into many other so-called variational problems. He opened up the mathematical investigation of minimal surfaces leading later to the Plateau Problem:
In spite of the fact that soap films seem to easily solve this question in the affirmative, for a long time all attempts at a mathematical treatment were disappointing. Lagrange himself indeed discovered the necessary conditions - so-called partial differential equations - that a minimal surface must satisfy at each of its points, but using the theoretical methods of that time, it was quite hopeless to try to answer his question in general. The degree of complexity of the occurring problems outreached the capabilities of the mathematical craftman's tools of those days and it urged mathematicians of the next generations to develop manifold techniques in different areas of mathematics. Among those were differential geometry, complex analysis, theory of partial differential equations and calculus of variations, to name the major fields contributing to minimal surface theory. |