This chapter addresses the award-winning NRICH project, a collaborative mathematics outreach initiative based at the University of Cambridge, UK.

Aims: NRICH aims to enrich and enhance the experience of the mathematics curriculum for all learners; develop mathematical thinking and problem-solving skills; offer challenging, inspiring and engaging activities; show rich mathematics in meaningful contexts; and. work in partnership with teachers, schools and other educational settings to share expertise.

What: NRICH is an innovative collaboration between the Faculties of Mathematics and Education at the University of Cambridge, part of the University’s Millennium Mathematics Project. Its online platform maps NRICH resources to the school curriculum, enabling all teachers to embed engaging, creative, rich mathematics in the reality of the classroom. NRICH also works face-to-face with teachers and their students, leading events at our base and further afield.

Why: Research highlights the urgent need for society to nurture future citizens with collaborative problem-solving skills which they will need to thrive in our increasingly automated environment (OECD). Although mathematics is a core curriculum subject up to age 16, too few students continue to study the subject at undergraduate level or beyond and there are ongoing concerns regarding the diversity those cohorts. There is a growing shortage of trained mathematics teachers in schools and frequently acknowledged negatively held attitudes towards mathematics in the wider society need addressing. NRICH project aims to address these issues by ensuring all learners have access to high quality resources which enthuse them about learning mathematics, address negative attitude and develop their key skills. The project is funded through grants and philanthropic donations.

How: The NRICH website publishes free resources for teachers which are publicised through online newsletters, social media platforms and the mathematical education community. NRICH also leads face-to-face teacher professional development to enable schools to maximise the potential of its resources and a hands-on schools roadshow where their learners can explore NRICH activities in their own settings. Schools are strongly encouraged to submit the work of their learners to the website, enabling each activity to have examples of classroom solutions which teachers can use with their classes in a multitude of ways, such as widening their classes knowledge of different approaches and providing an opportunity for their learners to communicate mathematically with an international audience of learners. NRICH has recently added webinars to its outreach work, bringing together learners from across the world to solve problems together.

Development: NRICH is a long-established mathematics outreach project. It was set up 20 years ago as a response to growing calls for an online mathematics club for children. This early version of NRICH evolved into today’s website where teachers can source free, high quality classroom resources for problem-solving. Today, NRICH uses Twitter and other social media platforms to communicate with its users on a much more regular basis than more traditional newsletters would allow, as well as increasing its use of YouTube videos and webinars.

Where: NRICH is based in the Centre for Mathematical Sciences, University of Cambridge. Its designers are experienced classroom teachers, supported by IT specialists and web designers who help to create our online community. The team work across the Faculties of Education and Mathematics, ensuring that NRICH has access to the latest international research to inform its work.

Impact: NRICH attracts over 30 million hits to its website each year. It has a growing presence on Twitter and recently set an unofficial world record for the largest-ever mathematics lesson across multiple settings. NRICH uses a combination of quantitative and qualitative measure to evaluate its impact. Our quantitative measures include website metrics which enable the team to monitor the usage of its resources online, including the time spent exploring activities and the number of times that users revisit them. NRICH also adopts qualitative measures such as focus groups and teacher interviews. For our face-to-face events we use pre- and post- questionnaires to measure their impact.(Show less)

The Institut Henri Poincaré is committed to an ambitious math communication project called Maison Poincaré. This house will be part of a completely refurbished building, and will include a permanent exhibition dedicated to mathematics and their interactions with other fields in science and technology. The project was initiated in 2016 and should be achieved by 2022. It has many special features compared to existing math/science museums.(Show less)

What: Shifting ideas of how we learn and understand inhabit current views supporting transdisciplinary education. Such perceptions suggest a greater need now for discussion on how science, technology, engineering and mathematics concepts (STEM) integrate with the arts across a range of learning settings (A). Thus, acknowledging STEAM. The acronym provides a neat catchall title for creative learning ecologies, where cultures of thinking, creative programming, and inventive teaching rely on play, curiosity, fearlessness and purpose, to incite memorable learning experiences (Ritchhart, 2015; Wagner, 2012). Key to our unique STEAM research and practice is the passion for connecting ideas through playful engagement with mathematics. A range of mathematical content is explored through physical activities related to making. Maeda (2012) argues, there is no greater integrity, no greater goal achieved, than an idea articulately expressed through something made with your hands. Endorsing that approach, our research philosophy emphasizes individual freedom to engage with mathematical concepts through making, by asking makers not only to make, but to think about and feel the mathematics underpinning their actions of making ‘in the moment’. Dewey (1938) describes such immersion as ‘erlebnis’. For instance, the perceived simplicity in making a ‘binary bug’ (STEAMpop project), reveals deep conceptual connections between the knowledge systems of biomimicry, binary, elementary geometry, non-linear relationships, crystallography, patterning, engineering and the elements and principles of design. This is not reductive learning, but rather, transformative constructivism, hybridized with the beauty of Consilience Theory (Wilson, 1999).

Goals: Our practice-based research reveals STEAM to be more than the promotion of balanced transdisciplinary learning, in which inquiry and problem-based methods unsurprisingly require creative and critical thinking. The projects we develop for delivery within education, community and corporate environments share one clear purpose; that is, to build intercultural capacity by harnessing the power of visual and creative arts as a strategy for understanding STEM concepts, particularly mathematics. The main objective of our work is to inspire knowledge building via unique co-creation experiences, replete with mathematical content. Beyond the STEAM acronym, we believe in asking ‘why’ and ‘what if’ regularly. In terms of raising public awareness, understanding or mathematical literacy, making continual and implicit STEM connections within an Arts context and vice versa, demonstrates how transdisciplinary learning shapes the development of personal and professional identity (English, 2016). We see math-making as a great leveler, unhinged from subject specific skill or expertise, and let loose amongst what is already known, and what could be discovered. Therefore, there is an element of risk inherent in undertaking any of our projects. Such exemplars are important for all ages engaging in a ‘learning by doing’ experience, as well as pre-service teacher education, and ongoing professional development for in-service teachers. Self-transformation may be the result of choosing to use one’s thinking hands with a view to making that important commitment to risk (Hargreaves, (1994), in Craft, 2015).

Why: Our work does not require purchase of STEM/STEAM specific technologies. Our motivation is contingent with the situation of ‘what if?’. Its driving force relies on engaging with imagination and curiosity. Through academic pedagogy and STEAM experience design, we have developed rich techniques for dynamic, flexible and responsive learning that promotes the notion of how STEM industries might benefit from integration with non-STEM work and practices. Embedding the Arts in STEM affords disruption of traditional modes of learning by fully integrating disparate content in ways that are imaginative, challenging and relate to real-world concepts. As current Australian Chief Scientist suggests, “no clever country would encourage its most STEM-literate people to pursue only traditional research paths” (Finkel, 2016, p. iv). Finkel goes on to say that his own experience would reveal that he found opportunities in unexpected places (Finkel, 2016).

Who & How: To date, we have designed and delivered math-making experiences to a range of groups, primarily targeting educators through professional associations, accreditation bodies and via request from individual institutions. Our math-making workshops contribute to the outreach activities of the University of Technology, crossing faculties of Science, Design, Education and Transdisciplinary Innovation. In schools, we provide professional learning sessions that are accredited by the New South Wales Educational Standards Authority (NESA). We believe our greatest reach, however, is related to the public events we present through collaboration with museums and community organizationssuch as Momath, National Museum of Mathematics (New York City), Vivid Sydney, Museum of Applied Arts and Sciences (MAAS), and local/regional Australian galleries. Experience consistency finds us using mathematical paper folding (origami sekkei) as a foundation for many of the projects presented to schools, tertiary institutions, and the general public. Building on the duality of simple/complex making associated with origami sekkei, our projects incorporate one or more STEM or Arts perspectives such as mechatronics, robotics, photoluminescence, body adornment, augmented reality and the creation of digital visual narratives. There is a constant dialogue between ourselves as facilitators, and collaborators such as Australian Indigenous mathematicians, academics, local artists, teachers and students. All participants in our workshops and events provide valuable feedback affording the evolution of our research and practice based on continued contribution to building innovative cultures of thinking. STEAMpop Signature Projects are generally delivered in 90 – 120 minute workshops. The following information is from our website:

• Lumifold focuses on a mathematical paper folding pattern using the Origami Sekkei technique. The Lumifold experience results in the creation of a stunning lamp which is an expression of biomimicry, elementary symmetries and iteration.
• The Binary Bugs experience involves makers engaging in a range of surface patterning and folding based on the mathematical concepts of binary, probability and symmetry. The bug construction demonstrates expression of biomimicry in the creation of physical beetle or bug-like forms. Depending on the making context, Binary Bugs can be illuminated via LED paper circuitry or simple LED units. They can be displayed individually or in a swarm!
• Hungry Birds is where paper engineering meets mechanical movement, electronics and coding. Hungry Birds enters the world of math-making interactive illumination! STEAMpop continues the flat to form experience, encouraging your thinking hands to create a sensor activated nest of bird-like forms that glow and move.

While our work is not limited to these three projects, they represent the basis for iterations developed in co-creation with teaching teams located in several NSW schools and the University of Technology Sydney. The activities also travel, as seen in Bridges Math Art conferences 2016 and 2019, Moves conference at Momath in 2017 and 2019, and at the School of the Arts Institute Chicago in 2016. We have presented aspects of the projects online through digital learning platforms and continue to build a visual presence on social media using Instagram and professional learning network via Twitter.

When & Where: Success of our transdisciplinary work has been measured quantitatively using survey instruments on completion of community workshops and more formally using Experience Sampling in our research in schools. The projects form part of Melissa’s doctoral research study, currently in the final stages of completion. Melissa’s research uses a mixed methods approach with emphasis on qualitative data collection. Loosely, the experiences we provide can be described as transformative, given that all participants journey through a range of emotions to rest at a point of completion grounded in challenging, interesting and fun-filled experiences. We like to think of our designed experiences as inventive flexibility, aligned with Craft’s (2015) appreciation of key aspects of a creative self being that “there are no rules, and that we ‘make it up’” (p. 85). While we are not extraordinary, we have an appreciation for mathematics that originated in the pursuit of an aesthetic encounter with material technologies. The material being paper, the technology being our hands, and the encounter simply representing an existential truth: mathematics underpins everything. Our connected curiosity has resulted in small extraordinary experiences for participants, so in this way, we are indeed, extraordinary.(Show less)

This project uses tools coming from graphic visualization, like graphic recording, sketchnotes and more traditional illustration, and a variety of social media platforms (blog, Twitter, Instagram) to communicate mathematical ideas and promote the role of women in mathematics. The project consist of a blog (The RAGE of the blackboard), and two Twitter/Ig 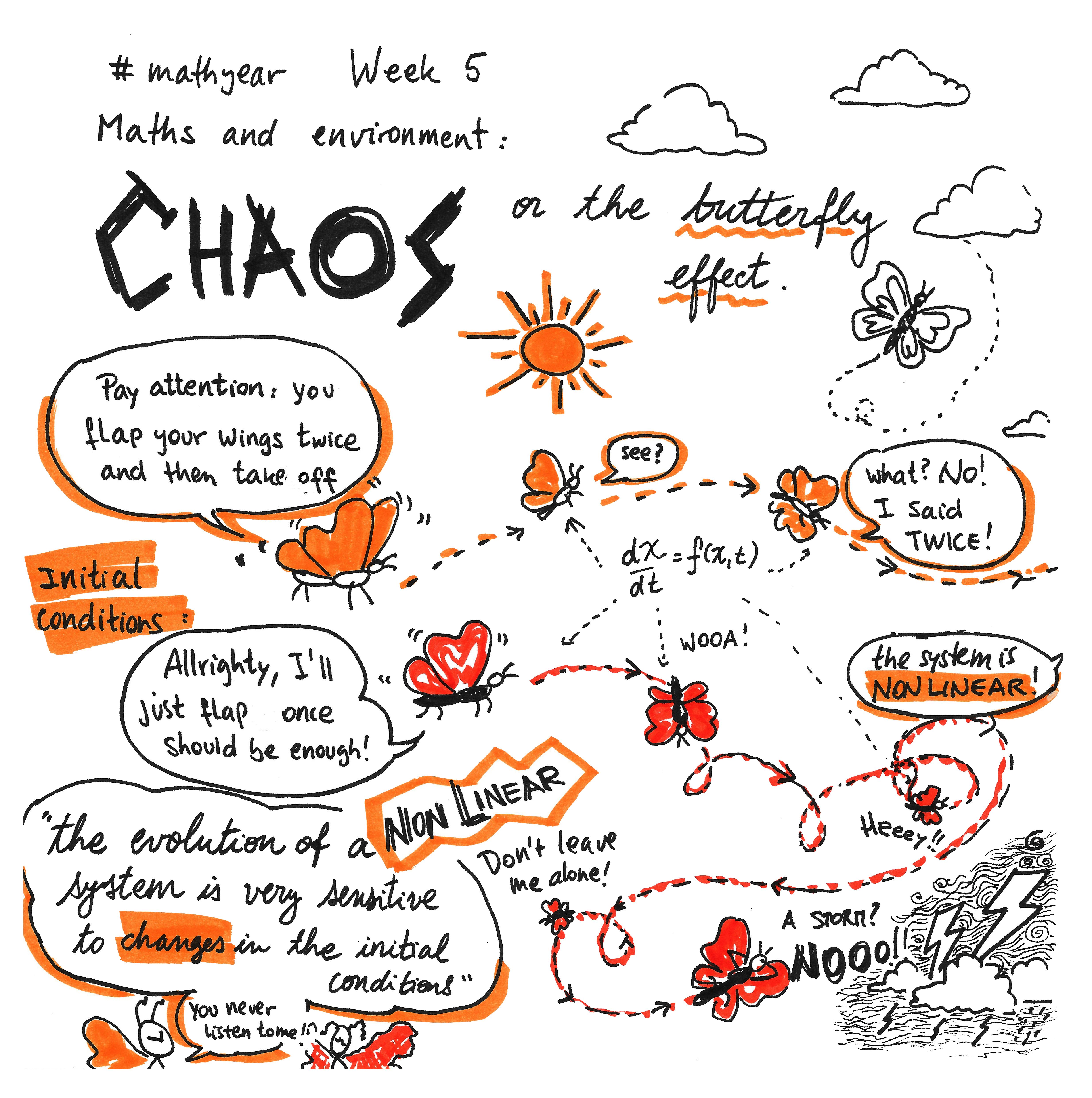drawing challenges: #Noethember, on the life and work of German mathematician Emmy Noether, and #mathyear, on the exploration of maths and its interactions.

The message: the blog promotes the role women mathematicians in science, giving details on their lives, their career paths and the obstacles they have faced, and on the impact of their work. The #Noethember and #mathyear projects are collective challenges with hand-drawn pictures that evoke specific mathematical ideas, in a playful and informal way.

The goal: to give a glimpse of the diversity in mathematics, in both the people that do maths and its applciations, in an original way that is visually appealing. This is in order to stimulate the audience's interest and curiosity to do further research, get interested in the topics or the people that do mathematics and look for more information aboute them.

The communicator and the audience: the project is carried out by the author, mathematician, lecturer at a public university. The Twitter challenges include collaborations (with one other person who also has a scientific background). The target audience is people in social media that already show an interested in science, as well as science communicators, academics, undergraduate and graduate students, teachers.

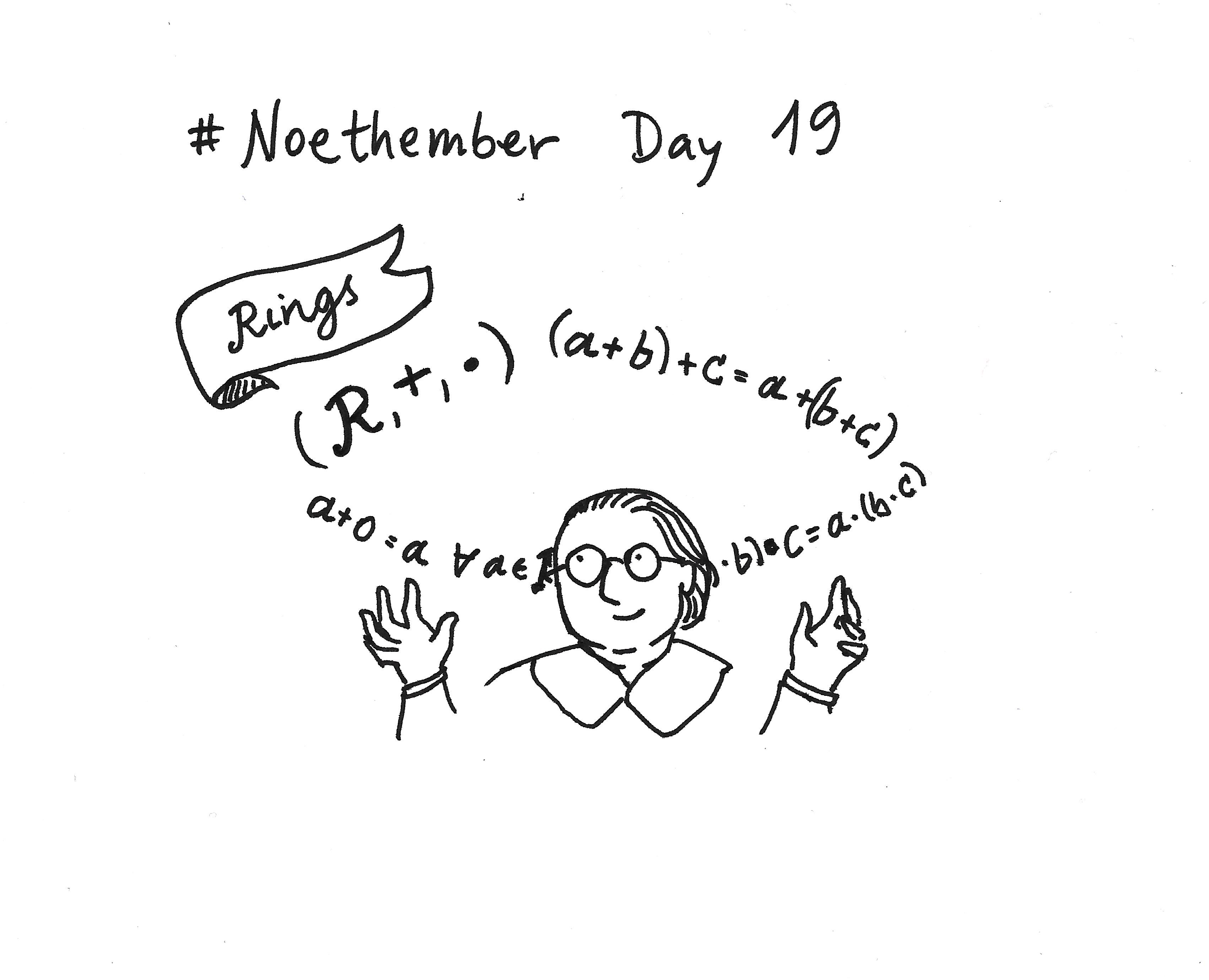
The motivation: the promotion of women in mathematics carried out in the blog is to help fill the gender gap seen in mathematics at undergraduate and graduate levels, but especially in academia at the level of assistant professors and full professors. The Twitter challenges aim to approach mathematics to the general public appealing to people's interest in image. There is no funding for this initiative, since it is not supported by any institution, and is done as a personal inititative.

The methods: the format of the blog interviews varies between traditional text and illustrations, and full sketchnotes. The Twitter challenges consist of hand-drawn images that convey information. These are regularly posted in social media, with some brief text giving context to the pictures. The post is followed by an invitation to the audience to participate by posting their own drawings tagged with hashtags that allow the author to track them in social media and repost them to promote the participant's work. This is inspired by the Inktober initiative, well known in the medium of professional illustrators.

Time frame: The blog project has evolved over time, and is used as a playground to test novel ways to portray female mathematicians and their work, as well as to promote other projects. #Noethember is a 30-days inivitative, while #mathyear is a 52 weeks project.

The location of the project is the internet, and it is written in English to reach an international audience. The way to measure the success of the projects is through likes, reposts and articles in websites specialized in science communication.(Show less)

In 2016, a math trail through Leiden (The Netherlands) was developed during a student project that was part of the specialisation Science Communication and Society, a Masters track at the Faculty of Science of Leiden University. The aim was to provide a math trail through the city, linking everyday sights to mathematical concepts within the curriculum of high school children. Next to this, the goal was to show children that mathematics is more tangible than the sums and problems they have to solve in school and to create more enthusiasm for the subject by bringing them in contact with mathematics outside the classroom.

The project time-frame was 3 weeks from the start of the project to the final presentation of the developed product. In this short time, background research had to be performed, the target audience to be determined, a route with questions designed and tested and the booklet to be designed and printed. At the end of the three weeks, this had all to come together in the form of a report and presentation.

The background consisted of a literature review, target audience surveys with school children and focus groups with teachers. Based on the conclusions from this background research we decided to change the target audience from the initial target audience proposed by the author of the project description. Afterwards, we developed a route, partly based on the knowledge of our group members about interesting historical sights in Leiden. Part of the questions were developed with the goal of coupling them to these sights. Other questions were included because of the curriculum of the children and later connected to the buildings and objects that we encountered while walking the proposed route. During the development of the questions, the goals to make the math trail a fun experience that makes math less abstract and to include questions from across the curriculum, were kept in mind.

In this chapter, we would like to share our insights from the background research and our experiences in developing a math trail. We show that in a short student project the process from background research to end product can be followed successfully and that the research assists towards achieving set goals within the final product. We moreover aim to provide those who are interested in designing a math trail in their city with a practical step-by-step plan and checklist.(Show less)

In 2010, five mathematicians founded the Institute for Computational and Experimental Research in Mathematics (ICERM), located on the campus of Brown University, Providence, RI, USA. The goal of ICERM is to promote computational methods and experiments in mathematical research. The institute does so by inviting topical programs to take place at ICERM over the course of several months.

From September to December 2019, the semester program Illustrating Mathematics took place at ICERM. This specific program brought together mathematicians, makers, and artists to find new forms of illustrations in and for mathematics. Driven by its exciting content, this semester program was able to reach out into the community and present its contents to a broader audience. The program website (https://icerm.brown.edu/programs/sp-f19/#publicoutreach) states:

“Objects created for mathematical visualization are beautiful and attractive in their own right. ‘Illustrating Mathematics’ brings together artists, makers, and mathematicians seeking to harness the creativity of mathematical illustrations to further the public’s understanding of mathematical research. ICERM invites you to engage with these talented artists-in-residence and explore their work. Visualize mathematics through displays of art made using 3D printing, laser cutting, CNC routing, virtual reality, textiles, carving, painting, video, and more!”

There were several events revolving around public outreach and mathematics communication during the program. They included an on-site and an off-site mathematical art exhibition, an ICERM open house during a STEM-themed city-wide Waterfire event, and five Math+Art panels featuring artist and mathematicians answering questions about how art and math relate from the audience. During Waterfire, and again later in the semester, the public were invited to participate in building two large mathematical sculptures in ICERM’s modern and open space.

The article discusses these events in details. Particular attention is given to organizational aspects and evaluation of the activities in hindsight. The broad range of events serves as a template for others, from which they can draw and learn.(Show less)

Motivation: My father, Luciano Emmer, was a famous Italian filmmaker. He made not only movies but also many documentaries on art, for example, a documentary with Picasso in 1954 and one about Leonardo da Vinci that won a Golden Lion at the Venice Film Festival in 1948. Although I knew I was to be a mathematician from a very young age, I was interested in film and I participated in a few of my father’s films. I graduated in 1970 and accidentally found myself working on minimal surfaces—soap bubbles—and had the idea of making a film. That was the start of the idea of the film series Art and Mathematics, produced by my father and Italian state television RAI. I learned much from my father, and I found myself a capable filmmaker, too.

Methods used: The Art and Mathematics project started in 1976. Or better, that is the year when I started thinking of the project. I was at the University of Trento in northern Italy. I was working in an area called the calculus of variations, in particular, minimal surfaces with Mario Miranda and I met Ennio De Giorgi, Enrico Bombieri and Enrico Giusti. All coming from the Scuola Normale Superiore in Pisa. In 1974 Bombieri received the Fields Medal. in 1976, I also met Jean Taylor who proved a famous result: the types of singularities of the edges that soap films generate when they meet. Plateau had experimentally observed that there are only two kinds of angles generated by soap films. With her and his husband Fred Almgren we decide to make a film on soap bubbles. In the same year I saw a large exhibition of the famous artist Max Bill, in particular the Endless Ribbon—an enormous Möbius band made of granite—was a real revelation. Its shape, its physical nature and its threedimensional reality made it live in space. It was a mathematical form—alive. So another idea for another film.

The idea: From the very beginning of the project there was the idea of focusing on the influence and the connections of mathematics and culture, using the most important visual tool: film. The idea was to show using a single theme, such as soap bubbles or topology, how the interests of artists and mathematicians are born and to see if it was possible to exchange ideas between scientists and artists—all this, however, following my father’s teachings of expressing ideas using images alone. I had to build a sequence of images that was first of all compelling from the point of view of cinema. A film is not an essay or a picture book. The visual documents fascinate per se. The idea then is to use few words and many images, applying all the possibilities of the language of cinema. All movies had to be really professional. The interest was also on the fiction films made involving history of mathematicians, inviting to the conference in Venice filmmakers like Peter Greenaway.

The audience: As these were the general outlines of the project, it was quite natural to consider as part of it the organization of exhibitions (many were presented in subsequent years), congresses, and completely new courses, including three years of teaching at the International School of Scientific Journalism at the SISSA in Trieste and a completely new course on Space and form, for student of the last year of math and in Industrial Design, for ten years, , seminars, and the publishing of books (with many illustrations!), and today, more than 45 years later, it is easy to say that the project went far beyond expectations. The last book by Springer will appear oin 2020, in 2019 the last two international exhibitions, the last congress on math and culture in Venice, and other books and papers. So the project is intended for really everybody. Hundred thousand of people have been involved: visiting the exhibitions, taking part in the congresses, hundred of students in courses, reading books by MIT Press, and Springer. Film have been translated in french, english, spanish and diffused all over the world.

Where: The films have been made in several countries around the world, from Japan to India to the USA and several countries in Europe with artists and mathematicians. Most of the conferences took place in Venice starting in 1997 and in Rome, where the first large exhibition of M. C. Escher was organized in 1985 together with the Dutch Government. Scientific committee included Roger Penrose and Donald Coxeter who both took part in my movie on Escher, 50 minutes, distributed in many countries including the USA. A second exhibition was organized in 1998 in Rome and Ravello. The proceedings of the first congress were published by Elsevier, of the second by Springer, reprinted several times.

When: It started in 1976 and the project is still going on, with the new book of Springer “Imagine Math 7” will appear in 2020, and the catalogue of the last very large exhibition on soap bubbles in art and science published in 2019 in Italian and English, with more than 40,000 visitors.

Comments: A film is not the best tool for explanation or learning. A film can, in a short amount of time, provide ideas and suggestions and create stimuli and emotions. A film can generate interest, even enthusiasm. Looking at an engaging, pleasant film can stimulate the audience to learn more, both in the artistic and the mathematics fields. In this sense I consider my films educational, but only with this meaning. This, on the contrary, is the secret of their success, as with the movie Soap Bubbles, even after 40 years. The most beautiful sequences indeed I have ever made—the soap films dancing to Invitation to the Dance (Le Spectre de la Rose) by Carl Maria von Weber—were included in the Video Math festival selection for the International Congress of Mathematicians in Berlin in 1998 and in the European Congress of Mathematics in Barcelona in 2000. And in 1986 it was shown at the Venice Biennale of Art. The movie is still circulating. In 2009 I wrote a 400-page book on soap bubbles in art and science that received one of the most important awards for an Italian essay, the Premio Letterario Viareggio. Ennio Moricone made the original music of the battle for my film in animation Flatland with real objects and the film was invited to several film festival and studied by films critics. The same for the Escher movies with many animations in 2D. (Show less)

STEAM-ing Up Learning with Experience Workshop in Finland and Around the World: Collaborations and Creative Discoveries Connecting Mathematics and Arts Education

The Experience Workshop – International Steam Network (www.experienceworkshop.org) had started in 2008 in Hungary and 2010 in Finland as a collaborative effort of mathematicians, artists, teachers, parents, and children. Experience Workshop is organizing various math-art-education events and interactive exhibitions, workshops, seminars, and training all over in Europe, and we have numerous educational and research collaborations in Africa, America, Asia, and Australia. Over the years, several tens of thousands of people participated in our projects.

On the one hand, connections between mathematics and the arts education provide Experience Workshop's pedagogical basis, on the other hand, we recognized the increasing need for STEAM (Science, Technology, Engineering, Arts, and Mathematics) integration in learning. The development of collaborative and inter-, multi-, and transdisciplinary problem-solving capabilities, which enable students to discover unexpected connections between different aspects of various complex phenomena, is not only a useful tool but recognized as one of the most important goals of today's learning societies. STEAM in today's European schools represents a dynamically developing, but mostly unexplored field. Based on a brief overview of the European "STEAM-scape," we introduce some of the major trends, opportunities, and current challenges of inter-, multi-, and transdisciplinary mathematics learning combined with various tools and technologies, as these trends are represented in Experience Workshop's daily practice. In accordance with the goals of the volume, we would like to highlight especially those components, which are enhancing the collaboration opportunities on the field of “mathematical arts and creativities” between diverse educational cultures from a global perspective. (Show less)

People’s views of mathematics are mostly shaped by their experiences in the mathematics classrooms and thus by their teachers. Therefore, teachers are or should be considered important maths communicators. But studies (e.g. TIMSS video study, see for example Baumert & Lehmann 1997) show that mathematics is mainly being taught via routine tasks, hence as algorithmic procedures, and exploring and problem solving are rarely present in most German classrooms (only 5 % of all exercises; ibid.). Teaching practices like this make it difficult to establish adequate views of and beliefs about mathematics.

To shape the views of students according to the beautiful, diverse and process-oriented scientific field of mathematics, to engage students with mathematics, and to enable them to apply it to their daily life, teachers themselves have to have appropriate beliefs and knowledge to be able to communicate and teach these in the classroom. Unfortunately, learning about other topics than those stated in the school curricula, about core competencies like problem solving and mathematical argumentation in detail, about recent mathematical research, and creative ways of communicating mathematics to their students are (currently) not part of the typical teacher education in Germany, at least not as mandatory classes. Therefore, teachers also should be considered a target group for mathematical science communication.

This chapter is guided by two relevant questions:

• What do teachers have to learn to be able to communicate mathematics adequately?
• How can we – as mathematics communicators ourselves – teach mathematical science communication for teachers?

To illustrate these questions, a university course, which has already been conducted, is presented.(Show less)

A lively scene of STEM activities and initiatives has arisen in Germany beyond the public school system during the last two decades. In this article, we make an inquiry on existing activities and initiatives in STEM subjects in Germany with a focus on the youth, Germany’s “Science Years” (“Wissenschaftsjahre”), the “Year of Mathematics” (2008) and its aftermath. We try to give an exhaustive outline on the existing activities but will not evaluate what’s being offered. We aim to show if or how the offer completes public education and ask for reasons for this extensive offer beyond the public school system that reaches from education to edutainment. Additionally, we outline trends in science communication in Germany with an emphasis on mathematics during the past 20 years.

Thomas Vogt has studied geology, German literature and science journalism in Berlin. He wrote freelanced articles for the Berlin daily newspaper DER TAGESSPIEGEL (1998), then was employed by Helmholtz Center Jülich (1999-2002), the German Aerospace Center and the Leibniz Association, where he was spokesperson, too. In his various positions, he contributed each year to the Science Years in Germany from 2000 (year of physics) to 2006 (year of computer science). In the year of mathematics (2008) he became a senior writer and editor on behalf of Deutsche Mathematiker-Vereinigung at the MCBO at Prof. Günter Ziegler’s chair. Today he is the spokesperson and head of the Math Media Office of the German Mathematical Society at Freie Universität Berlin, www.mathematik.de, Contact via medienbuero@mathematik.de (Show less)

Mathematics, or more precisely: mathematical research and its results, can in many ways play a role in and for mass publications, such as books, newspapers, magazines, radio, television, movies or online media. In our paper we will focus on two aspects: Mathematics can (1) be directly connected with the subject of the content. It can also (2) act indirectly as a catalyst, for example, to make reporting on some topic possible.

Mathematics as a Subject: A typical example for the former would be a report on a result from current mathematical research, usually about a topic with an attributed special news value for the readers. When mathematics is the core of the topic, this is usually disclosed to the recipients; mathematics is explicitly addressed. In which form this is done usually depends on, among other things, the topic and the news factor that is attributed to the topic in the respective medium, as well as on the narrative approach chosen by the respective journalist. This approach is also subject to changes in the journalistic understanding of roles. For example, while science journalists in the 1980s often showed themselves to be broadcasters of knowledge, science journalism at the turn of the millennium focused more on scientific content that was supposed to be useful in some way for the everyday life of the recipients. Currently, reporting and "checking" of facts are particularly important aspects.

Parts of mathematics can certainly connect to such trends and additionally serve various news factors. However, a large part of mathematical research is probably neither concretely applicable in the everyday life of the recipients nor can it be communicated to the recipients on a simple level. In addition, "mathematics" is strongly identified in the public with the contents of the correspondent school subject, which has little to do with current mathematical research. All of this means great changes, but also great challenges for a science that would like to see all of its facets reflected in mass media.

Mathematics as a Catalyst: Mathematics as a catalyst is a newer aspect and has in part only become possible with the upcoming of data scientists and people with mathematical training in newsrooms. Here, the mathematical operations are typically hidden in the background. In particular, examples can be found in the growing field of data journalism, which generates journalistic insights by evaluating data sources (such as statistics or measured values) and then presenting them to the recipients by illustrating them appropriately. Evaluation of data, gaining results and communicating the findings can each be based on the application of mathematical methods or tools from computer science. (One might, for example, think of the use of cluster algorithms in the visualization of data.) The mathematics behind it is not or only very briefly explained to the recipient, because it is not the core topic of the text; without this mathematics, however, the evaluation would not be possible in this form and depth.(Show less)

New York's National Museum of Mathematics: From 1980 through 2006, North America enjoyed only one museum devoted to mathematics: the Goudreau Museum in Herricks, Long Island. Moreover, though one could find over 300 science museums in this region, exhibitions with a focus on mathematics were few. Two years after the Goudreau closed, a team came together dedicated to creating a new, modern, hands-on museum to help rectify this lack of opportunities for young people (and the rest of their families, and their teachers, too) to explore the wonder, creativity, and beauty of mathematics in person.

This chapter will recount the formation and development of what became the National Museum of Mathematics (MoMath) in New York City. This story encompasses many of the fundamental aspects of the Museum's mission: Its ambition to provide as comprehensive picture of mathematics as possible encountering the reality of producing tactile, interactive activities for visitors yielded a subject matter emphasizing geometry with forays into numerous other topics, including elementary number theory, dynamical systems, probability, optimization, and symmetry. MoMath formulated positive presentations of mathematics as its goals, to show that "math is cool" (and more explicitly, math is fun, creative, and beautiful), that new math is created every day, that anyone can do mathematics, and that mathematics is open-ended. (The hope here is that these presentations can displace the stereotypes that math is boring, repetitive, and narrow; that it is "dry" and "dead"; and that only a select few are able to thrive in mathematics. However, MoMath attempted to avoid defining itself in terms of these negatives.)

Although MoMath began with and is centered on hands-on exhibits, it adopted multiple other modes of mathematical communication: brief highly-interactive classroom sessions for visiting students; large-scale public presentations by mathematicians; participatory family-activity nights; professional conferences; and a math puzzle/problem contest for adults, to name a few. Since the underlying motivation is to effect social change in the way people perceive and feel about mathematics, it's necessary to adopt as many modes of presentation as possible to reach a broad and diverse audience.

The success of efforts to change people's attitudes toward a topic are notoriously difficult to assess. The chapter will conclude with some indications of MoMath's effectiveness in this regard, together with noting some aspects, such as telling inclusive stories about the people involved with mathematics, which have remained a challenge for the institution. Hopefully these observations can serve to promote, enrich, and enhance other outreach efforts along broadly similar lines: North America is certainly large enough to support more than one museum focused on mathematics.(Show less)

Mathematical models have been used in political decision making for a long time. However, in the course of the ongoing digitalization of society and the subsequent surge in available data and methods to analyze them, the importance of mathematical knowledge in politics has increased drastically. In such diverse areas as criminal sentencing, welfare resource allocation, policing, child abuse detection and climate policy, mathematical analysis is used to inform decision makers or even carry out decisions automatically. Given this development and the impact on the lives of individuals, critical reflections on the relation between mathematics and politics are needed.

This chapter takes a sociological perspective in order to illuminate the various dependencies between mathematics and politics. It does so with the premise that mathematical science communication is not necessarily a one-way street. If engagement of mathematics with political institutions and the broader public is to succeed, it requires reflexivity regarding the ways in which the application of mathematical methods themselves can carry value judgments. From this perspective, the chapter gives an overview of both the role of mathematics in politics (i.e., where does mathematics become consequential in politics?) and of politics in mathematics (i.e., which political assumptions and implicit decisions are embedded in mathematical forms of knowledge generation?). It sketches the resulting need for mathematical experts to see themselves as having political agency and to be aware of the assumptions underlying the use of mathematical modeling in political contexts. From this perspective, political literacy of mathematical experts appears just as important as mathematical literacy of the general public. The often complex relation between mathematical modeling and politics is then described systematically - presenting recent research in sociology and science and technology studies - and illustrated through a number of case examples. Lastly, the chapter discusses recent attempts to achieve fairness, accountability and transparency in machine learning as a way in which the political consequences of mathematical modeling can be addressed within a mathematical framework, but also points out the limitations of such a perspective, underlining the need for a continued communicative effort to achieve a dialogue between mathematics experts and society.(Show less)

Conceptual underpinnings of algorithm/data literacy: a roadmap. Societal and economic processes between organisations and individuals are increasingly designed with algorithms. Examples are digital consumer scorings, digital nudges and dark patterns in marketing. These algorithm-based information architectures, more precisely their design, their interaction with individuals and the resulting dynamics, can empower but also manipulate. Therefore, political as well as civil society and consumer-specific debates are necessary. However, to take part in these debates and in the novel societal and economic processes, individual prerequisites are required. Various approaches to algorithm literacy and data literacy (such as media literacy, digital literacy, competencies in the digital world, information literacy, etc.) attempt to define these prerequisites, but ignore the overlap with existing research far too often and lack premises and links to theories of competence.

Taking into account the concepts that seek to formalise algorithm-specific preconditions, a roadmap is presented in order to develop a concept that serves both research and social debates. Differentiating integration and validation are the two most important factors.

The roadmap: From an existing general competence framework, fundamental competence fields can be isolated for the topic area of algorithms on the basis of the analysis of its characteristics and effects. On the one hand, it must be examined which existing concepts address these fields of competence at least in part. One example is risk literacy, which enables an individual to search for statistical evidence, reflect on it, evaluate it and act accordingly to his/her or others’ benefit. Overlaps between different concepts have to be identified and demarcations need to be made to the general competence framework. On the other hand, it has to be determined whether the state of the challenge - including interaction with data-based behaviour prediction and control based on machine learning - can be taken into account. To this end, a test scheme has to be formulated to determine whether this selective competence framework of existing (and possibly added) competence fields can be ecologically valid. If the selective competence framework - the factual selection - is justified, the premises - the motivational selection – need to be made explicit. One example is the wish that consumers can obtain quality-assured results when facing algorithms. Such premises are needed to determine competence goals (example: the consumer has the competence to act with regard to the provision of quality information by his scoring provider). Only with these goals can the competence levels be formalised, i.e. which standards should be achieved. This can range from awareness of systems to a commitment to algorithm regulation. It is then important to specify the competence contents implied by the chosen competence fields and the subject matter of algorithms (e.g. fairness of a classification) and to sharpen them to such an extent that quantitative reviews are possible. The level assignment has to be reproduced reliably with the selected contents in empirical tests. Standardisation studies would then be necessary. In addition to such efficiency proofs in diagnostics, randomised controlled (experimental) studies should prove the effectiveness of competence differences. Qualitative work is also needed here to explore the scope of competence differences, for example with regard to trust. The roadmap presented is purpose-oriented to substantiate education and regulation needs but also innovation potentials.(Show less)

Communicating Mathematical Content about Health Topics Effectively – The Power of Icon Arrays and Natural Frequency Trees. Graphical representations can facilitate the understanding of mathematical content, such as health statistics that are communicated in patient information. In this chapter, we describe the application of different graphical means and will in particular focus on the use of icon arrays and natural frequency trees. Icon arrays are already understood by children and made their way into school curricula. They can be used to explain the pros and cons of different medical interventions as well as their risks and are increasingly used in the media – albeit not often enough. Natural frequency trees allow for transparent representations of the effectiveness of medical tests and interventions.(Show less)

IMAGINARY is an international non-profit organization dedicated to math communication, based in Berlin (see https://about.imaginary.org). It originated in 2008 as a traveling exhibition created by the Oberwolfach Research Institute for Mathematics (MFO), as a means to communicate modern mathematics. The experiences of that original exhibition, its international expansion to dozens of countries, and what it implied in terms of innovation for the modern math communication have been described previously [for instance in Raising Public Awareness of Mathematics, Springer 2012].

In 2013, IMAGINARY experienced its first significant transformation from being one exhibition project to being a multi-exhibition project, an online platform, a community of users and partners, and a stable working team. That opened a period of even further expansion, a consolidation of the project’s open-source philosophy, and an exploration of new communication formats beyond the exhibitions.

In 2016, a second transformation took place when IMAGINARY became a German non-profit organization, independent of the MFO (which remained a shareholder). With an initial financial support of the Leibniz Association, IMAGINARY started as a company with the goal of self-sustainability, offering services to museums and foundations, creating exhibitions and other products on demand. In this last period 2016-2020, IMAGINARY has developed two full-fledged new exhibitions. At the same time, it has also diversified its projects to include workshops with school audiences, online outreach projects, conferences and events, IT services to museums, EU projects on educational innovation, and many others.

In the first part of our chapter, we will describe these transformations and the evolution of the IMAGINARY project. We have progressively refined the didactical approach that we wanted to follow, making us strong advocates of the so-called non-formal education. We now prepare outside-of-the-school workshops and also do teacher training for educators and science mediators. We also had to turn our attention to the demographics we were covering, from different regions and cultural environments to girls and women empowerment, from social inclusion to non-standard target groups. We had to revise our policies, balancing a strong commitment to free and open licenses with our paid services covering our work. We have also broadened our network of contacts and partners, now including not only academics and mathematicians but also companies, artists, museums, cultural mediators, etc.

In the second part of our chapter, we will take a closer look at a few of our latest projects that illustrate our standpoint and the path walked since our first exhibition in 2008. We will describe the exhibitions La La Lab - The Mathematics of Music (2019, see https://lalalab.imaginary.org) and I AM A.I. - Explaining Artificial Intelligence (2020, see https://www.i-am.ai). We will end with some of our ongoing projects and collaborations as of 2020, including the International Day of Mathematics (see https://www.idm314.org) and a new mobile museum on the mathematics of Climate Crisis (see https://10mm.imaginary.org).(Show less)

Mathematical Films: In this chapter, we explore the possibilities of presenting mathematical ideas and stories about mathematics and mathematicians through film. Mathematics is an abstract science, while cinema is first and foremost a visual art. Then how is it possible to present mathematical ideas in cinema?

How in depth can the mathematical ideas be such that the cinema audience can still appreciate (and understand) the film? Where is the line between telling nontrivial things and being too complicated? The mathematical knowledge of a potential audience can vary dramatically. How can a film incorporating mathematics be both informative for non-specialists and not trivial for mathematicians? How can you simply show complicated, abstract ideas?

Based on several feature-length, famous films incorporating mathematics as well as the documentary films we have produced over the past decade as part of the project in Collaborative Research Centre “Discretization in Geometry and Dynamics”, we explore the possibilities of using the language of cinema to talk about mathematics and mathematicians.(Show less)

Mathematics Adventure Land is a permanent exhibition in Dresden, Germany, located in the municipal technology museum Technische Sammlungen Dresden. It was established in 2008 as the result of a co-operation between the museum and the mathematics department of TUD, Dresden’s renowned university of technology. The total number of visitors is approaching one million.

The project was inspired by the world’s first mathematical science center, Albrecht Beutelspacher’s Mathematikum in Gießen, Germany. Some of our exhibits were bought from there, but many were also developed in-house and were unique (at least for a while). As in the Mathematikum, there are no explanatory texts on the exhibits, only a prompt to act, in a few words.

In this article we sketch the concept of the exhibition and also explain why we consider it a (necessary) form of science communication. The museum is constantly developing a variety of additional offers that complement the actual exhibits. This will be discussed in the second part of our presentation.(Show less)