- Calculating Machines in China and
Europe in the 17th Century
-
-The Western View
-
Klaus-D. Graf
Freie Universität Berlin, Institut für Informatik
Takustr. 9,14195 Berlin, Germany
In their contribution to this
conference, BAI Shangshu and Li Di have re-
ported about their rediscovery of ten
calculating devices from the late 17th
and/or early 18th century in the Beijing
Palace Museum. They did outstanding
research work on the structures and
functions, the origins and manufacturing
of their discoveries, which are a real treasure in
the world - wide history of
mechanical computing.
Many questions about
these Beiiing Calculating Machines
(BCM) remain
open. Obviously there were considerable
influences from Europe. One or more
machines may even have come from Europe as
a gift to the Emperor of China,
but it is also obvious that early developments
in Chinese mathematics and tech-
nology have played an important role in the making of
the machines.
The ten machines can be
separated into two classes. In the
first class,
disks or gear wheels are
the fundamental means for performing arithmetical
operations. The wheels have ten teeth and carry
circular representations of the
ten digits 0... 9. A special onetooth device handles
the carry problem. So basi-
cally these machines can only
be used to do additions. Subtraction
becomes
possible ' as well if additional
mathematical manipulations (such as 9-comple-
ments) are used. Multiplication and division can
also be supported if adequate
algorithms are applied. However, elementary
multiplications of single digits,
necessary in these algorithms,
have to be done mentally or with
Neper' s
bones. Of course this class corresponds
to the Schickard or Pascal type ma-
chines. In the following it will be referred to
as the Beijing Disk Calculating
Machine class-BDCM class.
The second class uses
Neper's bones as fundamental means. Basically
the
devices from this class realise multiplications
of multi-digit numbers with one
-digit numbers. They will be called Beijing
Rod Calculating - BRCM - in this
paper. This class corresponds to
similar devices known in Europe as "Schotts
Rechen Cylinder" [6],[11].
Growth of knowledge about the BCM until 1994
In the following I
would like to give a survey of
existing documentation
and publications about the machines
since 1962 and comment on these
using
observations from my short inspection
of some of the BCM and
information
from the European history of calculating
machines not considered so far. This
survey also reveals some of the special difficulties
in investigating the machines
due to language problems. problems
of access, intercultural and other
prob-
lems.
In 1962 a first
article by YAN Dunjie in the Chinese
language appeared,
reporting about two ancient calculating
machines in the Beijing Palace Museum
[1].
In 1978 eight
more such machines were discovered in
a storeroom of the
Palace Museum and examined by
Professor Bai from the Beijing
Normal Uni-
versity and Professor Li from the Inner Mongolian Normal
University.
In 1980 they published a
detailed description and interpretation of
all ma-
chines in the Palace Museum Journal No.
1, in the Chinese language, [2]. I
re-
ceived an English translation
by Miss WANG Gui-Rong in
1992, a German
translation was made in 1993 by Miss SUN Bingying [3].
In 1985 a
machine was shown to Owen Gingerich
from Cambridge, U. S.
A. , which he called a "Pascal-calculator"
[4]. This machine carried the in-
ventory number 141816 (Figure 1). Gingerich
supposes that it is a copy, made
two centuries ago, of a gift (from
Louis XIV?) to the Emperor of China,
Kang
Xi (1654/62 - 1722). 1 am doubtful about
this conjecture, as the addition work
of this machine (Figure 2) is
very different from the very well-known
Pascal
machines.


Fig.1
Fig.2
In 1989 two of the
BCM were exhibited in Brussels [5].
One of them was
No. 141816 again, from the
BDCM class. In his comments for
the catalogue
(objects 262 and 263) Paul
Demaerel asserts that this machine was
made in
France in the second half of the 17th
century, realizing an improved draft by
Christian Huygens made in 1659.
Demaerel indicates that Huygens
followed
the basic idea of Pascal. To me, again, this does not
seem very likely because
of the different type of the adding work.
The other device shown in Brussels
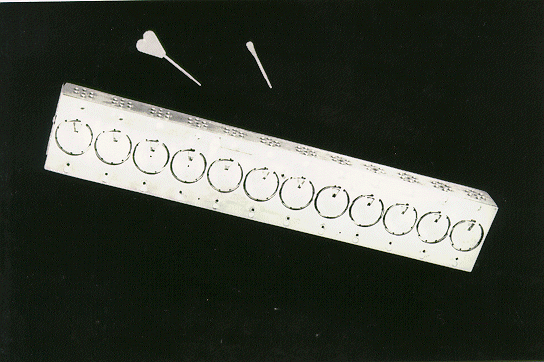
is from the BRCM class, with twelve
cylinders or drums (Figure 3). Fourteen
ivory rods - Neper's bones - are
mounted on each drum. Demaerel comments
that this machine was the answer
of Chinese scientists to Kang Xi's challenge to invent
a calculating machine for
multiplications, after having received machines for additions
from Europe. But
there are. European patterns for this type also, as mentioned
above (Figure 4).
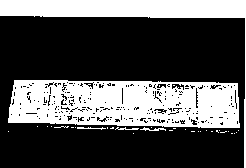
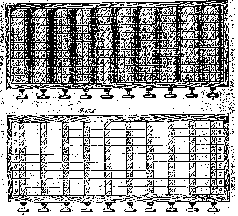
Fig.3
Fig.4
About 1988 Michael
R. Williams from Calgary, Canada, learned
about
the Beijing Calculating Machines from Bai
and Li. Among other things, they
discussed the problems of the origins. In 1992, as a
result of these contacts,
Williams, Bai and Li presented a summary
of the article from 1980 enriched
with some more remarks about
resemblances with Schickard's machine
and
Gaspard Schott's devices [7].
They also write that the BDCM
mechanism can work in reverse and so
al-
low subtraction "in a natural way" , 1. e. rotating the
disks anti-clockwise in-
stead of clockwise for addition. However, this contradicts
two other facts re-
lating to the BDCM, at least to No. 141816. Firstly,
the disks rotating under-
neath the surface of the machine, when a number from
I... 9 is entered, carry
two circular arrangements of the numbers 0... 9.
An outer ring runs anti -
clockwise, an inner ring runs clockwise,
so that 9-complements are respec-
tive neighbours. A sliding cover (in the window between
1 and 9 from the cir-
cle engraved on the surface over every disk) reveals
only one of the comple-
ments at a time. The same principle is true
for Pascal's machines. He does
subtraction by using konegative numbers.
This is necessary because his ma-
chine does not allow reverse input as Schickard's does.
Secondly, the example for carrying
out subtraction given by Bai and Li in
their contribution mentions clockwise movements
of the disks only. The de-
scription is not quite complete in all steps. I suppose,
however, that subtrac-
tion is indeed carried out in the "Pascal way" when using
the BDCM.
In 1991 I was lucky enough to
see three of the machines in Beijing [13].
I-They were No. 141816 and two of
the BRCM class. Unfortunately, I could
not make any photographs and not look into the
machines in detail. Also, at
this time I was not prepared to ask or to check
the questions in doubt men-
tioned so far. It is my impression that the machines
I saw were manufactured
in the Palace workshops. One reason for this is the Chinese
denotation of val-
ues for each of the wheels, transcribed with Latin letters.
The denotations in-
deed refer to a system of weights, as Gingerich
guessed. The unit " quian'
stands for 0. 17637 ounces, approx- 5 grams, possibly
a link to gold or silver
coins.
In 1992 I received some
photographs from Professor Bai showing two
dif-
ferent BDCM, one was No.
141816, and several BRCM. One
photo showed
part of the mechanism of No. 141816
(Figure 2). The photo of the adding
mechanism reveals a very special feature of No.
141816: the disks, each one
together with an auxiliary disk guaranteeing the right
direction of rotation of
the neighbour in case of a carry, are arranged on two
different levels. For this
reason the single teeth which transport the carries
are mounted alternatively
above and below the auxiliary wheels.
In 1993 Miss SUN Bingying
was able to inspect some of the
machines in
the Palace Museum and she confirmed these observations.
Bai and Li show this in a sketch
in their contribution.
This special feature does not
show up in Schickard's machine, at least not
in its modern realization by Baron
von Freytag-Lbringhoff. I suppose, how-
ever, that this feature can again be traced in a draft
of a calculation machine
which was made and published
by Jacob Leopold in 1727 [8] (Figure
5).
There are some surprising resemblances between this
draft and the No. 141816
BDCM. As well as the arrangement of the
wheels, their shape and the shape
of the shafts or axles also look similar, as do the positions
of the single teeth
for the carries as well. The Leopold draft also
shows the 9-complements sys-
tems on the wheels. There are
two differences, however: firstly, the No.
141816 BDCM forms a rectangular box,
while the Leopold machine is round.
Secondly, the Leopold draft is for a machine which
also allows multiplication.
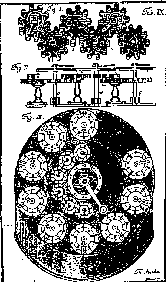
Fig.5
However, the resemblance in
the adding mechanism is surprising. So
pos-
si 'bly a link can be found from Leupold's
draft to the BDCM by further re-
search. It is known that Leupold's draft was taken
up in a machine by Anton
Braun about 1730 [9].
Areas to be explored for complete information about the BCM
For complete elucidation of all secrets of the BCM
one needs detailed in-
formation from at least three fields:
a) thorough
examination of all the BCM by experts
with mathematical.,
technical, historical or intercultural knowledge respectively;
b) a
survey of the scientific exchange and other activities
between Europe
and China before and after the reign of Kang Xi;
c) complete
information about the history of calculating devices
in Europe
and in China during the 17th century
and early 18th century.
a)
The activities mentioned before are only a beginning.
I do hope that
further actions will be taken by Chinese
scholars, cooperating with experts
from the West. The presentation of
the BCM at the IFIP Congress '94
in
Hamburg, can be a new starting point for this task.
b) European
scholars who lived 'n China for many years (such
as Jacques
Rho from Italy, -1625-1635,
Adam Schall from Germany,
~1630-1678,
Ferdinand Verbiest from Belgium, ~1660--~1675)
were of great influence in
the development of mathematics, astronomy and calendar
sciences in China. In
1628 J. Rho translated a book about calculation with
Neper's bones (1617) into
Chinese. These bones or rods soon became very popular
in China, and they
were modified and extended by Chinese mathematicians,
in particular by Mel
Wending who published a book about rod calculation in
1678.
The greatest influence on sciences
came from- French and German Jesuits
who were sent to China after 1685. They certainly
carried information about
European Disk Calculating Machines (e. g.
Pascal) and rod Calculating Ma-
chines (e. g. Schott) with them and they kept themselves
up to date by corre-
sponding with Jesuits in their home countries [7].
Considering facts such as
the possible relations with Leopold, which I mentioned
above, it is clear that
much more information is necessary about these links.
Kang Xi himself took very great
interest in these things and he invited the
Western scholars to give lectures to him in the Palace.
As a consequence, 53
books on Western sciences were edited by Su li Ching-yün.
A well-known link
was also Leibniz, who corresponded with
J. Bouvet
and others in Beijing about the dyadic system, its connections
with the hexa-
grams from the I Ching, about a
Chinese Academy of Science and possibly
about the l,eibnlz calculating machine. Leibniz also
sent a letter to Emperor
Kang Xi with suggestions about this Academy. Professor
Bai told me that one
of his colleagues had seen this letter in the Palace
Museum before 1965; it
seems to be lost now.
H. H. Goldstine mentions
that possibly a Leibniz calculating machine
was
sent to Kang Xi late in the 17th century [10].
No trace can be found of such a
gift today, not even in various lists of presents given
to Kang Xi, which were
checked by Bai and Li.
Checking the sources cited by
Goldstine, I have the impression that they
deal rather with plans to send a machine to Kang Xi via
Peter I of Russia than
with real activities.
c) In
the 15th century in Europe the respective algorithm methods
of cal-
culation were introduced together with
the Indian -Arabian decimal system.
The mechanising of these methods by
machines or machine-like devices start-
ed with two of the most important subroutines: firstly,
the digit by digit addi-
tion of two multi-digit numbers together with a suitable
transport of the car-
ries, and secondly, the multiplication of a
multi-digit number with a one -
digit number. Subtraction as well as general multiplication
and division could
then by realised by integrating adequate manual operations.
Pascal (1642) solved the
problem of addition with a mechanism
of pin-
wheels. The carries were transported
by a mechanism dependent on gravity.
As a consequence, subtraction could hot
be performed by running the wheels
backwards. Instead, konegative numbers had to be
applied. This is why the 9
-complement of each digit from 0... 9 is
exposed in the display windows as
well.
The mechanizing
of the multiplication problem mentioned
above was
solved with a device from Schott (1664) [6],
using a mechanism of cylinders
with a set of 10 or more of Neper's bones
mounted on them Fill. The trans-
port of carries showing up in this method
was not solved mechanically. (When
multiplying 47 * 3, e. g. , the carry 2 from
the partial product 21 must be
added to the partial product 12). The display of 1/2
2/1 on the cylinders had
to be changed "manually" to obtain the result 141.
Long before Pascal and
Schott, both problems were solved by
Schickard
(1623) with one machine, or rather two machines
in one box. The multiplica-
tion work was very much like Schott's, the
addition work consisted of teeth-
wheels with additional teeth for the carries. This
setting also permitted re-
verse input, thus subtraction could
be carried out without using 9-comple-
ments. Results from one mechanism had to
be moved to the other one manual-
ly.
Leibnlz (1672/74) constructed
the first machine which completely mecha-
nised all four types of calculation, using
teeth-wheels and the stepped-drum
mechanism invented by him [12].
The BDCM No.
141816 has an adding work with teeth-wheels
and one-
tooth wheels for the carries, which is rather similar
to Schickard's work. The
display, however, contains 9-complements like
Pascal's machine. I could not
yet find out if the mechanism can move in both directions,
and if not why not.
The draft of a calculating machine
by Leopold (1727) [8], [9] also shows
an adding work with teeth-wheels and special
teeth for the carries, and 9-
complements like No. 141816. I have commented on this
similarity before.
It does not seem to be known
whether Leopold had any earlier patterns in
mind. Schickard's machine was not one,
at least, because Leopold did not
know this machine. He knew the "Pascaline" , so
one cannot exclude the idea
that he changed Pascal's basic design into a machine
with teeth wheels and a
different carry device. The same conjecture may also
be true for the "Improved
version of Pascal's machine" attributed to Huygens
(according to the exposi-
tion in Brussels mentioned above).
The sketch just displayed, stressing
technical aspects instead of chronolo-
gy, may give some hints as to where to place the
BDCM. Obviously there is no
direct relation to Schickard, Pascal or Leibniz. So the
search for Chinese or
European sources of the special features of the
Beijing Disk Calculating Ma-
chines has to go on.

Beijing Disk Calculating Machine #141816

Beijing Disk Calculating Machine #141816

Beijing Disk Calculating Machine Inside
View
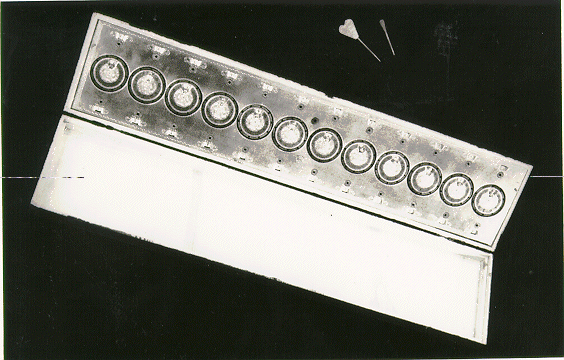
Beijing Disk Calculating Machine 12
Digits
Beijing Disk Calculating Machine 12
Digits

Neper's Rods Chinese Version

Neper's Rods Chinese Version

Beijing Rod Calculating Machine 12
Digits

Beijing Rod Calculating Machine 10
Digits, rods from paper
[1] YAN Dun-jie, 'Collection of Calculating Machines
of the Ching Dynasty in the Palace
Museum' (in
Chinese) , Cultural Relics, No. 3,1962.
[2] BAI Shangshu and Li Di, "Collection
of Original Hand Calculators in the
Palace Museum" (in
Chinese), J. Palace Museum,
No. 1, 1980.
[3] SUN Bingying, Translation
of the article [2] into German, Preprint
B 93 - 12, Fachbereich
Mathematik und Informatik der
Freien Universitit Berlin, Berlin 1993.
[4] Gingerich, O. , Instruments in the Beijing
National Palace, Bulletin of the Scientific Instrument Soc.
No. 10 (1986).
[5]" Chine - Ciel et Terre, 5000 Ans d'Inventions et
de Decouvertes" , Catalogue of an exposition of
Musees Royaux d'Art et d'Histoire,
Brussels 1988.
[6] Bischoff, J. P. : Versuch
einer Geschichte der Rechenmaschine, Ansbach
1804, newly edited bv
Stephan Weiss, Systhema Vertag,
Munich 1992.
[7] Li Di, Bai Shangshu, Williams, M. R., Chinese
Calculators Made During the Kangxi Reign in the
Qing Dynasty, Annals of the History of Computing,
Vol. 14, No. 4. 1992.
[8] Leopold, J. , Theatrum arithmetico-geometricum, Leipzig
1727, Reprint Hannover 1982.
[9] Kehrbaum, A. and Korte,
B. , Historische Rechenmaschinen im
Forschungsinstitut ftir Diskrete
Mathematik Bonn, Teil
1: Mathematiker und Rechenmaschinen,
DMV - Mitteilungen
1/93,
Tcibingen 1993.
[10]Goldstine, H. H. , The computer from Pascal
to von Neumann, Princeton University
Press,
Princeton, New jersey 1972.
[11]Williams, M. R. , From Napier to Lucas: The
Use of Napier's Bones in Calculating
Instruments,
Annals of the History of Computing,
Vol. 5, No. 3,July 1983.
[12]Williams, M. R. , A History of Computing
Technology, Prentice Hall, Englewood Cliffs,
N. J. 1985.
[13]Graf, K. D. ,
Rechenmaschinen aus dem 17. Jahrhundert in
China, DMV -Mitteilungen 1/94,
Tübingen 1994.