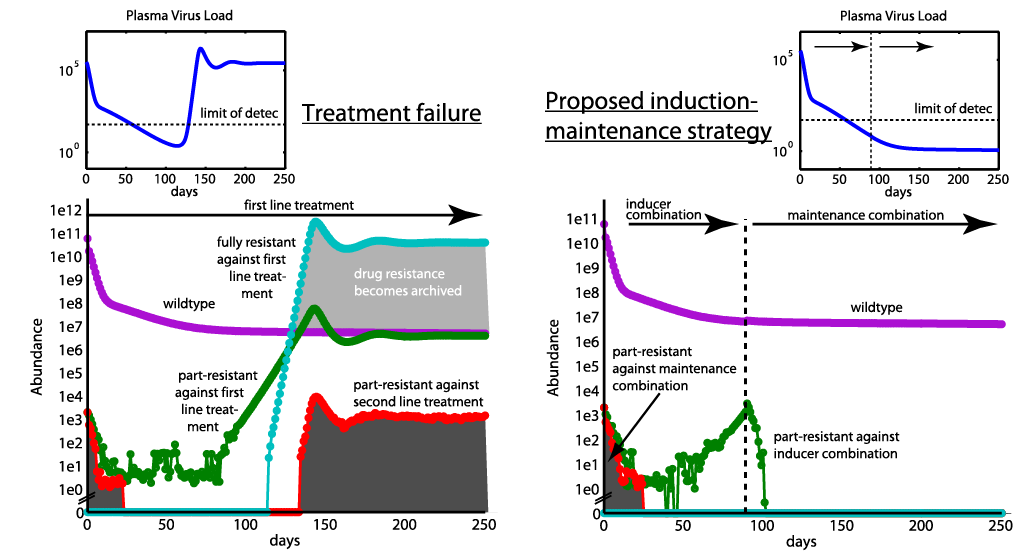
HIV can adapt to treatment pressure by developing drug resistance, which render treatment ineffective and put the patient in risk of death. Moreover, once resistance develops, it can infect persistent, long-lived cells (resistance "archivation"), limiting future treatment options for the patient. Therefore, an optimal treatment strategy should aim at minimizing resistance emergence and subsequent "archivation". In order to suggest an improvement to current treatment strategies, we followed a very simple idea: The greater the pool of replicating viruses, the greater the probability of resistance emergence. A strategy, which minimizes the pool of replicating viruses, while at the same time not selecting resistance, could therefore provide a long-term benefit to patients. Our idea was to use an "induction-maintainance" strategy: An initial treatment line (induction) was used with the sole purpose to lower the amount of replicating virus. This treatment line was replaced (before break-through and archivation of resistance) by a second treatment line (maintainance), which would now have a much better starting point, as the probability for resistance emergence against the maintainance treatment would be much lower (see figure above), mainly because the total virus population has been downsized by the first treatment line (induction). The difficulty lies in finding the "optimal" switching time, which poses a formidable mathematical task. The results of this project were published in PLoS One and intensively discussed in various community platforms, e.g. here.