Here are some clarifications and assumptions for making the problem more specific:
  1. A wall is a set of grid squares, i.e. a 1×n rectangle (not a line segment).
  2. At each integer time t=0,1,2,…, the puck is at the center of a grid square.
  3. A wall can be built or removed only at integer times.
  4. The puck can hit a wall or the edge of the field at times 1/2,3/2,5/2,….
  5. In boundary cases (grazing a wall, escaping through a corner, hitting a vertex head on), the puck is reflected (or not reflected) as follows:

    Figure 1:

On the right, there are three ways of trapping the puck with just one or two wall cells, in the middle or close to the corner of the field. Depending on the starting position of the puck, the second or third option may not be available. If it is o.k. for the wall to jump back and forth between two positions, even a single wall cell (T=1) is sufficient.

We address the grid squares as (x,y) from (0,0) (lower left corner) to (499,499), where x is the horizontal coordinate.

A solution of the original problem in less than 1150 steps

We have a total wall length of T=500 cells at our disposal. We assume the weakest model (the third model): We hear when a wall was hit, but not which wall it was or where it was hit.

At time t=50, we build a horizontal end-to-end wall of length 500 at height y=512, and wait till the wall is hit at some time t0+½, where t0≤50+2×512−1=1073. After it is hit, we build horizontal walls of length 10 with the left endpoints at (x,y) =(0,510), (10,509), (20,508), …, (490,461), in a staggered fashion, one wall at each step t0+1, t0+2, …, t0+50.

Figure 2:

If the puck is below the long wall, it will hit one of these short walls immediately after it is built. In that case, there are 12 potential locations of the puck and we can capture it quickly. We only show a solution for the last wall at y=461, which is hit at time t0+½+50. (The other cases are a bit more tricky, but more time is available to finish in these cases.) We build a facing wall and two detection bricks, as shown in Figure 2. By listening whether the puck makes one or two pauses after exiting through the corners, we can identify its position and cage it, after something like 23 additional steps, but there is certainly room for improvement in this endgame. More substantial savings are possible by placing the walls with a horizontal offset of 11 instead of 10, for example.

If no second hit occurred by time t0+½+50, we know that the puck is in the upper half. We have wasted 50 steps, but on the other hand, we know that t0≤50+2×487−1=1023. This stronger bound exactly balances the wasted time. We construct horizontal walls with their left endpoints at (x,y) =(0,564), (10,565), (20,566), …, (490,613), and the procedure runs exactly like in the lower half. The total time until the puck is confined is perhaps around 1073+50+23∼1146, with an error margin of one or two.

If it is an issue that we partially dismantle a completely built wall, we could build the initial wall of length 500 in portions of 10 bricks at a time. The case that the initial wall is put on top of the puck has not been discussed, but this is actually a lucky advantage: we know that the puck must be in a position as if it had just hit the wall, and we can immediately start the second phase without waiting.

Catching the puck in time 83505 with one wall cell (T=1)

If left alone, the puck follows one of 501 closed loops. 499 loops are tilted rectangles, and two are the diagonals of the field. Each loop is traversed in 1000 steps. If we place a wall anywhere, it will intercept 6 of these loops, unless it touches the boundary or straddles a diagonal. If we wait 1000 time steps after placing the wall, we are sure that the puck was not on one of these loops, and we should place the wall somewhere else.

Figure 3: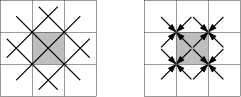

We put the wall on the 83 positions (3,1), (9,1), (15,1), …, (495,1) and wait 1000 units.

Figure 4: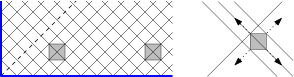

After 83 failed rounds of length 1000, at time 83001, only 3 potential tracks are left: two diagonal tracks, and one close to a diagonal. We place the wall near the center at (250,249) and wait, see Figure 4. After at most 501 steps, the puck must have hit the wall, and then it can be in one of 4 possible places and directions. After trying to block its way three times, we know precisely where it is, and we can confine it as described at the beginning.

A lower bound of 62500

There are 500×500×4=1000000 possible states of the puck (position plus direction). The 1000000 potential initial states lead, at any particular time t, to 1000000 different states. By placing the wall somewhere, it is possible to eliminate at most 16 states, either by placing the wall on the square with the puck, or by hearing the puck hit the wall 1/2 time step later (see Figure 3, right part). This gives a lower bound of 1000000/16=62500. (The above algorithm loses a factor of 16/12 over the lower bound because it mostly leaves the wall stationary, thus wasting 4 of the 16 states that potentially could be detected. It would be interesting to discover a strategy of constantly hopping around with the wall that would come close to the lower bound.)