|
Wie kännen Seifenhäute und Seifenblasen, mit einem Computer berechnet werden, wenn man keine expliziten Formeln dafür hat? Formeln sind schon für die meisten Seifenhäute unbekannt (obschon die Seifenhäute zu den einfachsten geometrischen Flächenklassen gehären und deshalb als Testflächen gern exemplarisch studiert werden), ebenso für viele andere Flächen in der Geometrie und in der Natur. In einem solchen Fall müssen numerische Verfahren angewendet bzw. entwickelt werden, um diese geometrischen Objekte am Computer zu studieren - sprich, die physikalische Welt muss im Computer simuliert werden. Allerdings gibt es nicht für jedes physikalische Problem ein einfaches Verfahren - zum Beispiel gehären instabile Seifenhäute zu den eher ungeliebten Kandidaten.
Wir mächten hier ein Konzept diskreter geometrischer Flächen vorstellen, bei dem charakteristische Eigenschaften von glatten Flächen auf diskreten Flächennetze definiert werden. Dieses diskrete Konzept [1][2][3] wurde in den letzten Jahren von mehreren Forschern entwickelt und hat schon erstaunliche Simulationen erlaubt, die äber die Fähigkeit von klassischen numerischen Verfahren hinausgehen - die weitere Entwicklung ist noch nicht abzusehen. Als Beispiel beginnen wir mit dem Münchener Olympiadach: dieses Dach erscheint von Ferne wie eine glatte Fläche - eine an mehreren Punkten aufgehängte gigantische Seifenhaut. Von Nahem betrachtet besteht das Dach jedoch aus einem Netz aus Drahtseilen, dessen Zwischenräume mit transparentem Material ausgefällt ist. Die äußere Form des Daches wird allein durch das Netz bestimmt. Hier wirken längs der Stahlseile, also längs der Kanten des Netzes, Zugkräfte und Spannungen, unabhängig von dem Zwischenmaterial, das erst zum Schluß in das Netz eingebaut wurde. Ferner beobachten wir, dass die auf jeden Netzknoten wirkenden Zugkräfte dort sich gegenseitig aufheben müssen, also ausbalanciert sind (ansonsten wärde sich dieser Knoten bewegen). In dem diskreten Konzept versuchen wir, diese Kräfte zu beschreiben und dadurch eine diskrete Seifenhaut zu definieren. Ein solches Konzept ist auch für andere Flächenklassen zu erwarten - dort herrschen dann natärlich andere Kräfte.
Diskretisierung von physikalischen Vorgängen gehärt zum Standardvorgang in der numerischen Mathematik wie bei Differenzenverfahren oder der Methode der Finiten Elemente. Deshalb ist es zur numerischen Untersuchung von glatten Kurven und Flächen mit Hilfe eines Computers unerläälich, dass man eine Mäglichkeit findet, diese geometrischen Objekte durch ein System mit endlich vielen Freiheitsgraden zu beschreiben (denn ein Computer kann in einem Programm nur endlich viele Zahlen bearbeiten). Was anfangs so technisch klingt, sieht in der Praxis oftmals sehr einfach aus: eine glatte Kurve wird zum Beispiel durch eine Folge gerader Stäcke ersetzt, oder eine glatte Fläche durch eine Menge von einfachen Dreiecken. Der Streckenzug ist eindeutig beschrieben durch die Menge von endlich vielen Eckpunkten (=Freiheitsgraden), die die geraden Kurvenstäcke begrenzen. Ebenso ist die triangulierte (d.h. aus Dreiecken bestehende) Fläche durch die endlich vielen Eckpunkte bestimmt, von denen jeweils drei benachbarte Punkte ein Dreiecke bilden.
Dieser Vorgang der Umwandlung eines glatten geometrischen Objekts heißt in der Fachsprache "Diskretisierung". Im Computer kännen jetzt die Positionen der endlich vielen Eckpunkte bearbeitet werden, und dadurch die 'diskrete' Fläche. Hierbei muss natärlich beachtet werden, dass die diskreten Flächen nur Annäherungen an die glatten Flächen sind, die man ursprünglich untersuchen wollte. Als wichtige Eigenschaft dieses Verfahren muss deshalb gewährleistet sein: bei feiner werdender Diskretisierung (also winzigen Strecken und Dreiecken), muss die diskrete Fläche der glatten Fläche immer ähnlicher werden, sie also approximieren. Die Gäte der Approximation kann man mit Hilfe verschiedenster Methoden messen, zum Beispiel kann der maximale Abstand der Punkte auf einem Streckenzug zur glatten Kurve als solches Maß dienen. Es ist allerdings oftmals schon bei einfach zu beschreibenden Probleme sehr schwierig zu gewährleisten, dass sich die Güte immer mehr verbessert, je feiner die Diskretisierung gewählt wird und schließlich die diskrete Fläche gegen ein glattes Objekt konvergiert. Die Entwicklung numerischer Verfahren und ein Nachweis ihrer Konvergenz bei feiner werdender Diskretisierung gehört zu den Standardaufgaben der numerischen Mathematik.
Einer der schwerwiegendsten Nachteile numerischer Verfahren ist die Tatsache, dass ihre Läsung eine äblicherweise glatte Situation nur approximiert. Sobald man nur an dieser Läsung interessiert ist, ist dieses Problem oftmals nicht weiter von Bedeutung - man kann die Diskretisierung feiner wählen, um "genauer" zu rechnen. Wenn allerdings die Läsung nur eine Subläsung ist, und es der Anwendung eines weiteren (oder mehrerer) numerischen Verfahrens bedarf, um sukzessiv aus der augenblicklichen Subläsung in einem nächsten Schritt eine weitere zu erzeugen und schlieälich zur eigentlichen Läsung zu gelangen, so kann auf diesem Weg soviel an Genauigkeit verloren gehen, dass die im letzten Schritt erhaltene Läsung mit dem Problem eigenlich gar nichts mehr zu tun hat- sie ist zu ungenau. Hieran kann oftmals auch die Wahl einer feineren Diskretisierung nichts ändern. Dies ist das Problem der Akkumulation von Ungenauigkeiten, wenn mehrere Verfahren nacheinander angewendet werden müssen.
Wir möchten jetzt ein anderes diskretes Konzept vorstellen, bei dem in erster Linie nicht versucht wird, eine glatte Situation zur approximieren. Stattdessen wird als erstes versucht, für das diskrete Objekt Eigenschaften zu definieren, und zwar unabhängig von der glatten, zu approximierenden Fläche. Betrachten wir als ein Beispiel wieder Seifenhäute und wählen eine Diskretisierung aus Dreiecken. Unser Konzept besteht jetzt darin, für eine solche diskrete Flächen Begriffe zu definieren, die die Fläche zu einer diskreten Seifenhaut machen: wenn die an jedem Punkt einer Fläche ausgehenden und geeignet gewichteten Kanten im Gleichgewicht sind, so nennen wir sie eine "diskrete Seifenhaut".
Betrachten wir als bekannteste Realisierung einer Seifenhaut in der Architektur wieder das Dach des Münchener Olympiastadions. Es ist technisch realisiert als ein Stahlseilnetz, das die Hauptlast der auftretenden Kräfte trägt, und in jedem seiner Knotenpunkte heben sich die auftretenden Kräfte auf. In unser diskretes Konzept übertragen heißt das: die mit den Zugkräften gewichteten Kanten stellen die längs jeder Kante wirkende physische Spannung dar. Damit das Gesamtsystem existieren kann, müssen sich diese Spannungen im Gleichgewicht befinden, d.h. in jedem Punkt müssen sich die Spannungen aufheben.
Die von uns benutzte Gewichtung der Kanten ist natürlich speziell für Seifenhäute. Andere Flächentypen benötigen andere Gewichtungen, oder sie müssen auf vollständig andere Weise charakterisiert werden. Es scheint aber vielfältige Anwendungsmäglichkeiten für solche diskreten Beschreibungen in praktischen Anwendungen zu geben, die auf ihre Entdeckung warten.
Flächen in der Natur und Technik sind immer mannigfachen äußeren Einwirkungen ausgesetzt, die unabhängig von ihren eigenen Eigenschaften auftreten. Seifenblasen und Zeltdächer sind zum Beispiel der Gravitation und Wettereinflßssen ausgesetzt, die als äußere Kräfte auf die Flächen wirken. Hier kommt die Eigenschaft der Stabilität ins Spiel: erst wenn die Flächen gegenüber kleinen Veränderungen stabil sind, können sie in der Natur existieren - ansonsten würden Seifenblasen beim geringsten Windstoß zerplatzen oder Zeltdächer bei Regen zusammenbrechen. Die einzige geschlossene Seifenblase in der Natur ist die runde Kugel, sie ist als einzige geschlossen Seifenhaut stabil und kann deshalb im physikalischen Experiment erzeugt werden. In der Mathematik betrachte man Seifenhäute und Flächen in einer idealen, abstrakten Umgebung, frei von den Widrigkeiten der Natur. Auf diese Weise treten in der Mathematik auch viel mehr verschiedene Arten von Seifenblasen auf - zum Beispiel die komplizierte Blase in Figur [Penta]. Sie ist instabil und besitzt außerdem Selbstdurchdringungen längs der Verbindungsstellen der äußeren zur mittleren Kugel, schon aus diesem Grund kann es sie nicht als physikalische Seifenblase geben. Es war lange Jahre ein ungelöstes Problem, ob neben der Kugel überhaupt andere geschlossene Seifenblasen existieren. Numerische Experimente haben keine anderen Flächen auffinden können, unter anderem, weil man mit ihnen meistens nur stabile Flächen erhält. Neben vielen theoretischen Entdeckungen konnte hier die diskrete Beschreibung von Seifenblasen einen entscheidenden Schritt weiterhelfen [3]. Mit ihr gelang es, mathematische Transformationen auf den diskreten Gittern durchzuführen und damit eine große Klasse von Flächen erstmalig zu berechnen und neue geschlossene Seifenblasen numerisch zu entdecken [4]. Diese Flächen sind faszinierendes Zeugnis dafür, wie neue Simulationstechniken überraschende neue Entdeckungen hervorbringen.
Vor wenigen Jahren war die heute bekannte Vielfalt an Seifenhautformen gänzlich nicht erwartet worden. Seifenhäute haben die Eigenschaft von holomorphen Funktionen in der Mathematik, d.h. sobald man eine Fläche an einer Stelle etwas verändert, so hat dies gleich (im allgemeinen unvorhersehbare) Auswirkungen überall auf der Fläche. Ein gezieltes Modellieren und Konstruieren von Flächen zum Beispiel durch das Verbinden zweier nahgelegener Seifenblasen mittels eines zylindrischen Henkels zu einer neuen Seifenblase schien unmöglich zu sein.
Umso überraschender waren die Entdeckungen in der Geometrie in den letzten Jahren. Einige Aspekte und Beispiele der gefundenen Flächen sind in dem Artikel "Die Geometrie von Minimalflächen" von H. Karcher und K. Polthier beschrieben [6]. Auch hier gelangen in den letzten Jahren weitere Fortschritte in der numerischen Simulation komplizierterer Seifenhäute durch neuen Algorithmen, die diskrete Beschreibungen der geometrischen Flächen verwenden.
Neue numerische Konzepte für sich zeitlich verändernde Flächen wurden ebenso entwickelt. Dies ermöglicht über die Beschreibung von statischen Flächen hinaus die Behandlung von sich deformierenden Flächen. Im Video "Palast der Seifenhäute" [5] sind einige der spektakulärsten Flächen gesammelt, und es bietet eine elementare Einfährung und einen unterhaltsamen Überblick über die verschiedensten Formen und Eigenschaften von Seifenhäuten. Man begleitet den kleinen Jungen Kalle bei seinen Abenteuern im Palast und erhält vom Professor Einblick in tiefere Zusammenhänge. In diesem mathematischen Spielfilm ist alles computergraphisch erzeugt, vom Seifenhautexperiment bis hin zum Flug durch unendliche Minimalflächen.
Video " Palast der Seifenhäute "[5]: Auf dem
Kirmesplatz bestaunt der kleine Junge Kalle die faszinierenden Erscheinungsformen von
Seifenhäuten in der Architektur. Im Hintergrund hängende Dächer ähnlich dem Dach des
Münchener Olympiastadions. Die meisten im Video gezeigten Flächen wurden mit Hilfe der
neuen diskreten Techniken erzeugt.
Penta-Fläche: Die Kugel ist die einzige Gestalt, in der eine
geschlossenen Seifenhaut in der Natur auftreten kann. Bis 1984 galt es in der Mathematik
als fraglich und ungelöstes Problem, ob weitere geschlossene Seifenhäute überhaupt
existieren können. Mittlerweile konnten weitere Beispiele gefunden werden. Die
Penta-Fläche[4] ist eine kürzlich numerisch entdeckte Seifenblase von recht einfacher
Gestalt- eine instabile Seifenblase mit Selbstdurchdringungen, die im Experiment sofort
zerplatzen würde. Sie wurde mit Hilfe eines numerischen Verfahrens [3] berechnet, das auf
dem im Artikel erwähnten diskreten Konzept beruht.
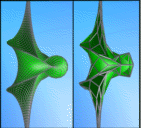
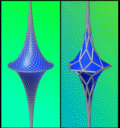Kähnsche Fläche und
Pseudosphäre: Diskrete Beschreibungen existieren mittlerweile für mehrere
geometrische Flächenklassen. Fischreusen sind ein charakteristisches Beispiel für
Flächen mit konstanter negativer Krümmung. Die hier gezeigte Pseudosphäre und Kühnsche
Fläche gehören zu dieser Flächenklasse. Beide Flächen sind in zwei unterschiedlichen
Diskretisierungen gezeigt, wobei jeweils auch die feinere Geometrie ein diskretes Objekt
darstellt: die Flächennetze erfüllen in jedem Gitterpunkt eine Balancebedingung, die im
Grenzfall unendlich feiner Diskretisierung der Definition von konstanter negativer
Krümmung glatter Flächen entspricht.[2] (Bild: Tim Hoffmann, TU-Berlin)
[1] U. Pinkall, K. Polthier Computing Discrete Minimal Surfaces and Their Conjugates Exp. Math. 2.1 (1993)
[2] A. Bobenko, U. Pinkall Discrete Isothermic Surfaces J. Reine Angew. Math. (1996)
[3] B. Oberknapp, K. Polthier An Algorithm for Constant Mean Curvature Surfaces in "Visualization and Mathematics" H.-C. Hege, K. Polthier (eds.) Springer Verlag Heidelberg 1997
[4] K. Große-Brauckmann, K. Polthier Compact Constant Mean Curvature Surfaces Exp. Math. (1996)
[5] A. Arnez, K. Polthier, M. Steffens, C. Teitzel Palast der Seifenhäute (Video, 41 min.) Bild der Wissenschaft (1995) (siehe: http://www.polthier.info/video.html)
[6] H. Karcher, K. Polthier Die Geometrie von Minimalflächen Spektrum der
Wissenschaft 10 (1990)