The Mobile Collection
Balanced on Occasion of
Hermann Karcher's
60th Birthday
The mobile collection is a set of five minimal surfaces with rather diverse properties and history. It is a random collection of surfaces with close connection to Hermann Karcher's work, each surface selected by mathematical as well as aesthetical criteria. The surfaces were numerically created in Berkeley, Erlangen and Freiburg, and manufactured by the company Ziemendorf GmbH in East-Berlin using stereolithography technique.
Here is a copy of this page with pictures and videos of the real models.
 |
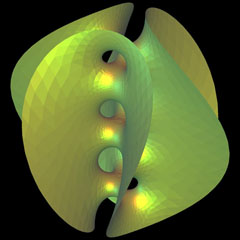
Less-Symmetric Scherk Saddle Tower (image
top left) The classical minimal surfaces of H.F. Scherk were found around 1835 in an
attempt to solve Gergonne's problem, a boundary value problem in the cube. The Scherk
surfaces were among the first candidates in Karcher's experiments to modify the
Weierstrass formula of existing surfaces. He selectively increased or decreased symmetry,
or twisted, or changed the topological genus by inserting new handles. The less-symmetric
saddle tower originates from Scherk's saddle tower with triple symmetry and modifying the
asymptotic angle of the half plane wings. |
|
|
|
 |
Chen-Gackstatter-Karcher-Thayer Surface Chen
and Gackstatter discovered in 1982 surfaces of genus one and two each having an
Enneper-type end of winding order three. Karcher found that the end may be generalized to
have any odd winding order. Thayer constructed numerically surfaces with many more
handles, i.e. higher genus, up to 35, and each can have a generalized Enneper-type end.
The triply symmetric surface of the mobile has genus six and winding order 5. |
|
|
|
 |
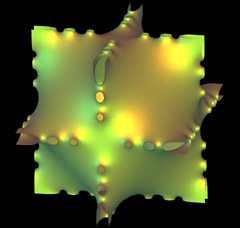
Lawson Surface of Genus 4 Lawson
constructs compact minimal surfaces in the 3-sphere of arbitrary genus by applying
Morrey's solution of the Plateau problem in general manifolds. This work of Lawson
contains a rich set of ideas among them the conjugate surface construction for minimal and
constant mean curvature surfaces. Karcher elaborated and perfected the conjugate surface
construction to allow the construction of a large number of new minimal and constant mean
curvature surfaces in different space forms. |
|
|
|
 |
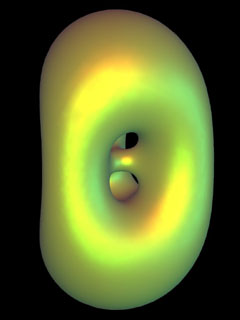
Neovius Surface with Additional Handles In
the last century H. A. Schwarz and his pupil E. Neovius were among the first to
specifically design new triply periodic minimal surfaces using complex analysis and the
Weierstrass representation formula. The physicist A. Schoen found many more triply
periodic surfaces in crystallographic cells. Karcher elaborated the conjugate surface
construction to proof existence of Schoen's surfaces, and many new examples. Karcher's
modification of Neovius' surface was numerically continued by Oberknapp to add a wealth of
handles. |
|
|
|
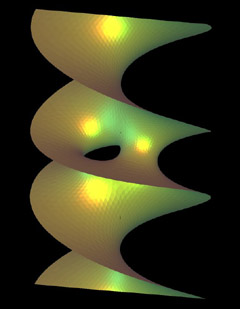 |
Hoffman-Karcher-Wei Helicoid The Genus-One Helicoid
is a minimally embedded torus with one end and infinite total curvature. More than 200
hundred years after the helicoid of Meusnier a new embedded minimal surface with finite
topology and infinite total curvature was found in 1993. Crucial to their new discovery
was the characterization of the Gauss maps' essential singularity at the end of the
helicoid. It is known that the initiative to the genus-one helicoid is due to Harold
Rosenberg: "Hermann, why don't David and you sit down and construct such an
example?" |