Klaus-D. Graf
Freie Universität Berlin, Institut für Informatik
      Takustr. 9,14195 Berlin, Germany

     In their contribution to this conference, BAI  Shangshu  and  Li Di  have  re-
ported about their rediscovery  of  ten  calculating  devices  from  the  late  17th
and/or early 18th century  in  the  Beijing  Palace  Museum.  They  did  outstanding
research work on  the  structures  and  functions,  the  origins  and  manufacturing
of their discoveries, which are a real treasure in  the  world  -  wide  history  of
mechanical computing.
     Many  questions  about  these  Beiiing  Calculating   Machines   (BCM)   remain
open. Obviously  there  were  considerable  influences  from  Europe.  One  or  more
machines may even have come from Europe  as  a  gift  to  the  Emperor  of  China,
but it is also obvious that early developments  in  Chinese  mathematics  and  tech-
nology have played an important role in the making of the machines.
     The ten machines can be  separated  into  two  classes.  In  the  first  class,
disks  or  gear  wheels  are  the  fundamental  means  for  performing  arithmetical
operations. The wheels have ten teeth and  carry  circular  representations  of  the
ten digits 0... 9. A special onetooth device handles  the carry  problem.  So  basi-
cally these  machines  can  only  be  used  to  do  additions.  Subtraction  becomes
possible '  as well  if  additional  mathematical  manipulations  (such  as  9-comple-
ments) are used. Multiplication and division  can  also  be  supported  if  adequate
algorithms are  applied.  However,  elementary  multiplications  of  single  digits,
necessary  in  these  algorithms,  have  to  be  done  mentally  or  with  Neper'  s
bones. Of course  this  class  corresponds  to the  Schickard  or  Pascal  type  ma-
chines. In the following it will be referred to  as  the  Beijing  Disk  Calculating
Machine class-BDCM class.
     The second class  uses  Neper's  bones  as  fundamental  means.  Basically  the
devices from this class  realise  multiplications  of  multi-digit  numbers  with  one
-digit numbers. They will be  called  Beijing  Rod  Calculating  -  BRCM  -  in  this
paper. This  class  corresponds  to  similar  devices  known  in  Europe  as "Schotts
Rechen Cylinder" [6],[11].
 

Growth of knowledge about the BCM until 1994

     In the following  I  would  like  to  give  a  survey  of  existing  documentation
and  publications  about  the  machines  since  1962  and  comment  on   these   using
observations  from  my  short  inspection  of  some  of  the   BCM   and   information
from the European  history  of  calculating  machines  not  considered  so  far.  This
survey also reveals some of the special difficulties  in  investigating  the  machines
due  to  language  problems.  problems  of  access,  intercultural  and  other   prob-
lems.
     In 1962 a  first  article  by  YAN  Dunjie  in  the  Chinese  language  appeared,
reporting about  two  ancient  calculating  machines  in  the  Beijing  Palace  Museum
[1].
     In  1978  eight  more  such  machines  were  discovered  in  a  storeroom  of  the
Palace  Museum  and  examined  by  Professor  Bai  from  the   Beijing   Normal   Uni-
versity and Professor Li from the Inner Mongolian Normal University.
     In 1980 they published a  detailed  description  and  interpretation  of  all  ma-
chines in the Palace Museum  Journal  No.  1,  in  the  Chinese  language, [2].  I  re-
ceived  an  English  translation  by  Miss   WANG   Gui-Rong   in   1992,   a   German
translation was made in 1993 by Miss SUN Bingying [3].
     In  1985  a  machine  was  shown  to  Owen  Gingerich  from   Cambridge,   U.   S.
A. , which  he  called  a  "Pascal-calculator"  [4].  This  machine  carried  the  in-
ventory number 141816  (Figure  1).  Gingerich  supposes  that  it  is  a  copy,  made
two centuries ago, of a  gift  (from  Louis  XIV?)  to  the  Emperor  of  China,  Kang
Xi (1654/62 - 1722). 1 am  doubtful  about  this  conjecture,  as  the  addition  work
of this machine  (Figure  2)  is  very  different  from  the  very  well-known  Pascal
machines.
  
                                Fig.1                                            Fig.2

     In 1989 two  of  the  BCM  were  exhibited  in  Brussels  [5].  One  of  them  was
No.  141816  again,  from  the  BDCM  class.  In  his  comments  for   the   catalogue
(objects  262  and  263)  Paul  Demaerel  asserts  that  this  machine  was  made   in
France in the second half  of  the  17th  century,  realizing  an  improved  draft  by
Christian  Huygens  made  in  1659.   Demaerel   indicates   that   Huygens   followed
the basic idea of Pascal. To me, again, this does not seem  very  likely  because
of the different type of the adding work.
     The other device shown in Brussels is  from  the  BRCM  class,  with  twelve
cylinders or drums (Figure  3).  Fourteen  ivory  rods  -  Neper's  bones  -  are
mounted on each  drum.  Demaerel  comments  that  this  machine  was  the  answer
of Chinese scientists to Kang Xi's challenge to invent a calculating machine  for
multiplications, after having received machines for additions  from  Europe.  But
there are. European patterns for this type also, as mentioned  above  (Figure  4).
 
                Fig.3                                                    Fig.4

     About  1988  Michael  R.  Williams  from  Calgary,  Canada,  learned   about
the Beijing Calculating Machines from  Bai  and  Li.  Among  other  things,  they
discussed the problems of the origins. In 1992, as a result  of  these  contacts,
Williams, Bai and Li presented a  summary  of  the  article  from  1980  enriched
with  some  more  remarks  about  resemblances  with  Schickard's   machine   and
Gaspard Schott's devices [7].
     They also write that the BDCM mechanism can  work  in  reverse  and  so  al-
low subtraction "in a natural way" , 1. e. rotating the disks anti-clockwise  in-
stead of clockwise for addition. However, this contradicts two  other  facts  re-
lating to the BDCM, at least to No. 141816. Firstly, the  disks  rotating  under-
neath the surface of the machine, when a number from I... 9  is  entered,  carry
two circular arrangements of the numbers 0...  9.  An  outer  ring  runs  anti  -
clockwise, an inner ring  runs  clockwise,  so  that  9-complements  are  respec-
tive neighbours. A sliding cover (in the window between 1 and  9  from  the  cir-
cle engraved on the surface over every disk) reveals  only  one  of  the  comple-
ments at a time. The same principle  is  true  for  Pascal's  machines.  He  does
subtraction by using konegative  numbers.  This  is  necessary  because  his  ma-
chine does not allow reverse input as Schickard's does.
     Secondly, the example for carrying out subtraction given by Bai  and  Li  in
their contribution mentions clockwise  movements  of  the  disks  only.  The  de-
scription is not quite complete in all steps. I suppose, however,  that  subtrac-
tion is indeed carried out in the "Pascal way" when using the BDCM.
     In 1991 I was lucky enough to see three of the  machines  in  Beijing  [13].
I-They were No. 141816  and  two  of  the  BRCM  class.  Unfortunately,  I  could
not make any photographs and not look into  the  machines  in  detail.  Also,  at
this time I was not prepared to ask or to  check  the  questions  in  doubt  men-
tioned so far. It is my impression that the  machines  I  saw  were  manufactured
in the Palace workshops. One reason for this is the Chinese  denotation  of  val-
ues for each of the wheels, transcribed with Latin letters. The  denotations  in-
deed refer to a system of weights,  as  Gingerich  guessed.  The  unit  "  quian'
stands for 0. 17637 ounces, approx- 5 grams, possibly a link to  gold  or  silver
coins.
     In 1992 I received some  photographs  from  Professor  Bai  showing  two  dif-
ferent  BDCM,  one  was  No.  141816,  and  several  BRCM.   One   photo   showed
part of the mechanism  of  No.  141816  (Figure  2).  The  photo  of  the  adding
mechanism reveals a very special feature of  No.  141816:  the  disks,  each  one
together with an auxiliary disk guaranteeing the right direction of  rotation  of
the neighbour in case of a carry, are arranged on two different levels. For  this
reason the single teeth which transport the  carries  are  mounted  alternatively
above and below the auxiliary wheels.
     In 1993 Miss SUN Bingying  was  able  to  inspect  some  of  the  machines  in
the Palace Museum and she confirmed these observations.
     Bai and Li show this in a sketch in their contribution.
     This special feature does not show up in Schickard's  machine,  at  least  not
in its modern realization  by  Baron  von  Freytag-Lbringhoff.  I  suppose,  how-
ever, that this feature can again be traced in a draft of a  calculation  machine
which  was  made  and  published  by  Jacob  Leopold  in  1727  [8]  (Figure  5).
There are some surprising resemblances between this  draft  and  the  No.  141816
BDCM. As well as the arrangement  of  the  wheels,  their  shape  and  the  shape
of the shafts or axles also look similar, as do the positions of the single teeth
for the carries as well. The Leopold draft  also  shows  the  9-complements  sys-
tems on the  wheels.  There  are  two  differences,  however:  firstly,  the  No.
141816 BDCM forms  a  rectangular  box,  while  the  Leopold  machine  is  round.
Secondly, the Leopold draft is for a machine which  also  allows  multiplication.
 
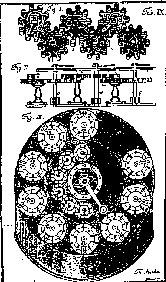
                                                       Fig.5

     However, the resemblance in  the  adding  mechanism  is  surprising.  So  pos-
si 'bly a link can be found  from  Leupold's  draft  to  the  BDCM  by  further  re-
search. It is known that Leupold's draft was taken  up  in  a  machine  by  Anton
Braun about 1730 [9].
 

Areas to be explored for complete information about the BCM

For complete elucidation of all secrets of the  BCM  one  needs  detailed  in-
formation from at least three fields:
     a)     thorough  examination  of  all  the  BCM  by  experts  with  mathematical.,
technical, historical or intercultural knowledge respectively;
     b)     a survey of the scientific exchange and  other  activities  between  Europe
and China before and after the reign of Kang Xi;
     c)     complete information about the history of  calculating  devices  in  Europe
and in    China during the 17th century and early 18th century.
     a)      The activities mentioned before are  only  a  beginning.  I  do  hope  that
further actions will be taken by  Chinese  scholars,  cooperating  with  experts
from the West. The  presentation  of  the  BCM  at  the  IFIP  Congress  '94  in
Hamburg, can be a new starting point for this task.
     b)     European scholars who lived 'n China  for  many  years  (such  as  Jacques
Rho  from   Italy,   -1625-1635,   Adam   Schall   from   Germany,   ~1630-1678,
Ferdinand Verbiest  from  Belgium,  ~1660--~1675)  were  of  great  influence  in
the development of mathematics, astronomy and calendar  sciences  in  China.  In
1628 J. Rho translated a book about calculation with Neper's  bones  (1617)  into
Chinese. These bones or rods soon became very  popular  in  China,  and  they
were modified and extended by  Chinese  mathematicians,  in  particular  by  Mel
Wending who published a book about rod calculation in 1678.
     The greatest influence on sciences  came  from-  French  and  German  Jesuits
who were sent to China after 1685.  They  certainly  carried  information  about
European Disk Calculating Machines  (e.  g.  Pascal)  and  rod  Calculating  Ma-
chines (e. g. Schott) with them and they kept themselves up to  date  by  corre-
sponding with Jesuits in their home countries [7].  Considering  facts  such  as
the possible relations with Leopold, which I mentioned above, it is  clear  that
much more information is necessary about these links.
     Kang Xi himself took very great interest in these things and he invited  the
Western scholars to give lectures to him in the Palace.  As  a  consequence,  53
books on Western sciences were edited by Su li Ching-yün.
     A well-known  link  was  also  Leibniz,  who  corresponded  with  J.  Bouvet
and others in Beijing about the dyadic system, its connections  with  the  hexa-
grams from the I  Ching,  about  a  Chinese  Academy  of  Science  and  possibly
about the l,eibnlz calculating machine. Leibniz also sent a  letter  to  Emperor
Kang Xi with suggestions about this Academy. Professor  Bai  told  me  that  one
of his colleagues had seen this letter in the  Palace  Museum  before  1965;  it
seems to be lost now.
      H. H. Goldstine mentions that possibly  a  Leibniz  calculating  machine  was
sent to Kang Xi late in the 17th century [10].  No trace can be found of such a
gift today, not even in various lists of presents given to  Kang  Xi,  which  were
checked by Bai and Li.
     Checking the sources cited by Goldstine, I have  the  impression  that  they
deal rather with plans to send a machine to Kang Xi via Peter  I  of  Russia  than
with real activities.
     c)     In the 15th century in Europe the respective  algorithm  methods  of  cal-
culation were  introduced  together  with  the  Indian  -Arabian  decimal  system.
The mechanising of these  methods  by  machines  or  machine-like  devices  start-
ed with two of the most important subroutines: firstly, the digit by  digit  addi-
tion of two multi-digit numbers together with a suitable  transport  of  the  car-
ries, and secondly, the multiplication of  a  multi-digit  number  with  a  one  -
digit number. Subtraction as well as general  multiplication  and  division  could
then by realised by integrating adequate manual operations.
     Pascal (1642) solved the  problem  of  addition  with  a  mechanism  of  pin-
wheels. The  carries  were  transported  by  a  mechanism  dependent  on  gravity.
As a consequence, subtraction  could  hot  be  performed  by  running  the  wheels
backwards. Instead, konegative numbers had to  be  applied.  This  is  why  the  9
-complement of each digit from 0...  9  is  exposed  in  the  display  windows  as
well.
     The  mechanizing  of  the  multiplication   problem   mentioned   above   was
solved with a device from Schott  (1664)  [6],  using  a  mechanism  of  cylinders
with a set of 10 or more of  Neper's  bones  mounted  on  them  Fill.  The  trans-
port of carries showing up in this  method  was  not  solved  mechanically.  (When
multiplying 47 * 3, e. g. , the carry 2  from  the  partial  product  21  must  be
added to the partial product 12). The display of 1/2  2/1  on  the  cylinders  had
to be changed "manually" to obtain the result 141.
     Long before Pascal  and  Schott,  both  problems  were  solved  by  Schickard
(1623) with one machine, or rather  two  machines  in  one  box.  The  multiplica-
tion work was very much like Schott's,  the  addition  work  consisted  of  teeth-
wheels with additional teeth for the carries.  This  setting  also  permitted  re-
verse input, thus  subtraction  could  be  carried  out  without  using  9-comple-
ments. Results from one mechanism had  to  be  moved  to  the  other  one  manual-
ly.

     Leibnlz (1672/74) constructed the  first  machine  which  completely  mecha-
nised all four types of calculation,  using  teeth-wheels  and  the  stepped-drum
mechanism invented by him [12].

     The  BDCM  No.  141816  has  an  adding  work  with  teeth-wheels  and  one-
tooth wheels for the carries, which is rather similar to  Schickard's  work.  The
display, however, contains 9-complements  like  Pascal's  machine.  I  could  not
yet find out if the mechanism can move in both directions, and if  not  why  not.

     The draft of a calculating machine by Leopold (1727)  [8],  [9]  also  shows
an adding work with teeth-wheels and  special  teeth  for  the  carries,  and  9-
complements like No. 141816. I have commented on this similarity before.

     It does not seem to be known whether Leopold had  any  earlier  patterns  in
mind. Schickard's machine  was  not  one,  at  least,  because  Leopold  did  not
know this machine. He knew the "Pascaline" ,  so  one  cannot  exclude  the  idea
that he changed Pascal's basic design into a machine  with  teeth  wheels  and  a
different carry device. The same conjecture may also be true  for  the  "Improved
version of Pascal's machine" attributed to  Huygens  (according  to  the  exposi-
tion in Brussels mentioned above).

     The sketch just displayed, stressing technical aspects instead of  chronolo-
gy, may give some hints as to where to place the  BDCM.  Obviously  there  is  no
direct relation to Schickard, Pascal or Leibniz. So the  search  for  Chinese  or
European sources of the special features of the  Beijing  Disk  Calculating  Ma-
chines has to go on.


   Beijing Disk Calculating Machine #141816
 

    Beijing Disk Calculating Machine #141816
 

    Beijing Disk Calculating Machine Inside View
 

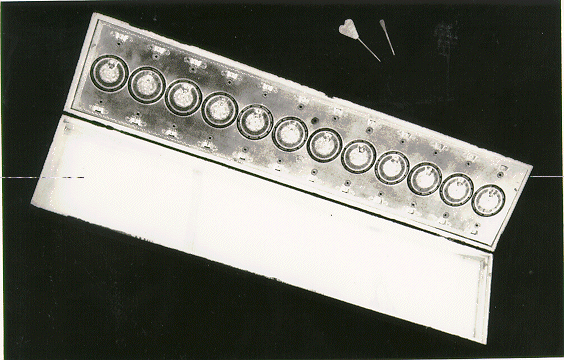
    Beijing Disk Calculating Machine 12 Digits
 

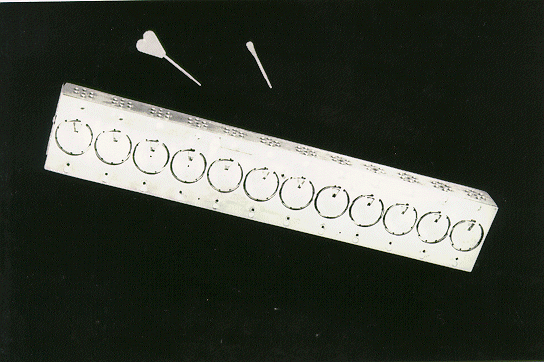
    Beijing Disk Calculating Machine 12 Digits
 

    Neper's Rods Chinese Version
 

    Neper's Rods Chinese Version
 

    Beijing Rod Calculating Machine 12 Digits
 

    Beijing Rod Calculating Machine 10 Digits, rods from paper
 

                                  References

[1]  YAN Dun-jie, 'Collection of Calculating Machines of  the  Ching  Dynasty  in  the  Palace  Museum'  (in
Chinese) , Cultural Relics, No. 3,1962.
[2] BAI Shangshu  and  Li  Di,  "Collection  of  Original  Hand  Calculators  in  the  Palace  Museum"  (in
     Chinese), J. Palace Museum, No. 1, 1980.
[3]  SUN  Bingying,  Translation  of  the  article  [2]  into  German,  Preprint  B  93  -  12,  Fachbereich
     Mathematik und Informatik der Freien Universitit Berlin, Berlin 1993.
[4]  Gingerich, O. , Instruments in the Beijing National Palace, Bulletin of the Scientific Instrument  Soc.
     No. 10 (1986).
[5]" Chine - Ciel et Terre, 5000 Ans d'Inventions et de Decouvertes" , Catalogue of an exposition of
     Musees Royaux d'Art et d'Histoire, Brussels 1988.
[6]  Bischoff, J.  P.  :  Versuch  einer  Geschichte  der  Rechenmaschine,  Ansbach  1804,  newly  edited  bv
     Stephan Weiss, Systhema Vertag, Munich 1992.
[7]  Li Di, Bai Shangshu, Williams, M. R., Chinese Calculators Made During the Kangxi Reign  in  the
  Qing Dynasty, Annals of the History of Computing, Vol. 14, No. 4. 1992.
[8] Leopold, J. , Theatrum arithmetico-geometricum, Leipzig 1727, Reprint Hannover 1982.
[9]  Kehrbaum,  A.  and  Korte,  B.  ,  Historische  Rechenmaschinen  im   Forschungsinstitut   ftir   Diskrete
Mathematik   Bonn,   Teil   1:   Mathematiker   und   Rechenmaschinen,   DMV    -    Mitteilungen    1/93,
     Tcibingen 1993.
[10]Goldstine, H. H. , The computer from  Pascal  to  von  Neumann,  Princeton   University   Press,
     Princeton, New jersey 1972.
[11]Williams, M. R. , From Napier to Lucas: The  Use  of  Napier's  Bones  in  Calculating  Instruments,
     Annals of the History of Computing, Vol. 5, No. 3,July 1983.
[12]Williams, M. R. , A History  of  Computing  Technology,  Prentice  Hall,  Englewood  Cliffs,  N.  J.  1985.
[13]Graf,  K.    D.  ,  Rechenmaschinen  aus  dem  17.  Jahrhundert  in  China,  DMV   -Mitteilungen   1/94,
     Tübingen 1994.