THE EFFECT OF COMPUTERS

Introduction

     Historical Sketch and Trends
     The  three  traditional  cultural  techniques  (Kul-
turtechniken),  which  play  the  most  important  role
in our children's education are  reading,  writing  and
calculating.  From  the  time  of  their   "definition"
(perhaps  1200  years  ago;  Alkuin,  an   adviser   of
Charlemagne,  mentioned  them)  the  sets  of   methods
establishing  these  techniques  have  undergone  great
changes and so did the subsets  which  were  accessible
at school levels. In our times  the  largest  expansion
occurred in calculating, which developed into  a  tech-
nique  of  solving  problems  formally  with   numbers,
symbols, graphics and  words.  On  one  side,  this  is
a result  of  extensive  mathematical  research,  which
among  other  results  brought  about  powerful   algo-
rithms, easy to execute. On the other side  this  trend
was accelerated by the rise of powerful processors  for
algorithms,  namely  computer  systems  together   with
their scientific  background,  informatics  (i.e.  com-
puter science). These aids make  a  variety  of  formal
problem-solving methods  accessible  for  school  math-
ematics and  other  subjects,  which  previously  could
not be executed  by  students  and  pupils.  Algorithms
form one important class of these methods.
     The development  outlined  above  caused  and  still
has a significant  impact  on  school  mathematics  ed-
ucation. At least three of  the  didactical  dimensions
of the mathematics  classroom  are  envolved:  content,
method and medium,  to  say  nothing  of  the  pupil  -
teacher relationship.  Control  on  these  impacts  can
only be  gained  by  integrating  and  organising  them
into mathematics curriculum at all  levels,  since,  as
A. Ralston [1990] points out  "  ..  only  ..  curricu-
lum content can serve as a  lever  to  change  the  en-
tire  mathematics  education  system".   Computer   use
in mathematics education  started  as  a  very  special
method  with  mostly  special   topics.   Future   com-
puter use should  be  a  standard  method,  applied  in
whole strands of subject  matter.  This  -article  will

give a review of some effective  and  successful  steps
and some reasonable  trends  in  the  pursuit  of  this
goal in school mathematics.

     In addition, many  of  the  examples  of  this  pa-
per indicate that the technology is already a  signifi-
cant factor in school classrooms, a  factor  that  more
than deserves  its  place.  The  contribution  that  it
can make to the social  and  academic  interactions  is
vivid and, once experienced, always valued.

     Finally, just as children play  out  a  wide  range
of roles in being part of the community  they  are  in,
so too  can  computers.  Thus  we  ask  the  reader  to
consider the computer as  a  member  of  the  classroom
community, one  that  is  able  to  contribute  to  the
day's activities in an appropriate fashion.

     Considerations  and  concrete  suggestions  for  the
use  of  computers  in  mathematics   teaching   depend
on  knowledge  about  and  experience  with  such   in-
struments  shared  by  teachers  and  mathematics  edu-
cators. Fifteen years ago these people  had  access  to
computers  mostly  as   programmers   in   numerically-
oriented  languages.  So  computing  power  was  mainly
used in secondary  math  education  for  numerical  al-
gorithms in the  form  of  short  Basic  programs.  Ten
years ago, another step - but still in the  algorithmic
spirit - was taken  with  Logo  on  various  home  com-
puters with  its  underlying  philosophy  of  exploring
mathematics  in  specially  designed  microworlds   and
of learning mathematics by  teaching  it  to  the  com-
puter; Logo also  included  the  use  of  geometry  and
symbolic  manipulations.  Primary  education  was   in-
volved with these ideas, even kindergarten.

     The proliferation  of  so-called  standard  software
on personal computers  in  the  last  decade  gave  wav
to  new  considerations  and  experiments,   especially
with  spreadsheets,  programs  for   data   representa-
tion, statistical and  numerical  packages,  databases,
CAD   (Computer   Aided   Design)-software   and   com-

puter  algebra  systems.  But  in   the   beginning   such
software  was  not  very  user-friendly,  and   afterwards
became  too  complex;   the   need   soon   became   obvi-
ous  for  special   school   adaptations   which   allowed
easy   specializations,   employed   mathematical    nota-
tion similar to that  used  at  school,  and  used  power-
ful  and  helpful  metaphors,  so  that  even  users  with
little training and only occasional practice (as  is  typ-
ical of  school  users)  could  succesfully  handle  them.
This  led  to  the  creation  of  general  and  didactical
software  tools  which  sometimes  also  had  a   tutorial
component,  thereby   integrating   some   traditions   of
computer-aided  instruction   (CAI).   All   these   forms
of  using  the  computer  came  into  being  in   sequence
but  can  now  be  found  simultaneously  in   discussions
about mathematics teaching.
     Even  if  suitable  hardware  and  software  are   now
available for  ordinary  schools,  several  necessary  in-
gredients are  still  missing:  Teacher  training  is  far
from sufficient; hardware  availability  in  most  schools
is still dictated by the needs  of  computer  science  and
computer   awareness   courses   and   the   concentration
of  machines  in  special  locations  prevents  or   makes
difficult the natural, selective use of software - e.g.  a
function plotter - during short  episodes  in  the  teach-
ing process.
 
 

     Influences on the Goals and Aims of
     Mathematics Teaching

     In  elementary  schools  children   meet   basic   pro-
ceases wi 'th  patterns  and  numbers  in   the   mathemat-
ir-s classroom for the first time. There  is  a  range  of
uses  of  technology  that  have   proved   positive   and
stimulating  in  helping   children   to   express   them-
selves and  to  progress  in  a  confident  and  enjoyable
fashion. In particular  these  can  help  to  discovery  -
partly unconsciously  -  of  the  importance  of  underly-
ing  structures  as  an  aid  to  qualified  communication
in  language  and  problem  solving.   The   computer   is
well-suited to setting up structures - this  will  be  il-
lustrated in the examples that  are  discussed  in  detail
in  the  section  on  Illustrative  Software  below.  (For
a  more  comprehensive  discussion  of  the  influence  of
computers  on  mathematics  teaching,   see   the   survey
by Fey, 1989.)
 
   The   emergence   of   multimedia   technology    means
that   our   communication   with   computers   and,   in-
deed,  amongst  ourselves  will  employ  words,   pictures
and sound in  equal  partnership  and  will  not  be  lim-
ited  to  a  fixed   sequential   presentation.   Although
this article draws  on  the  experience  of  using  micro-
computers in the  classroom,  it  will  also  be  relevant
to  the  more  sophisticated  interactive  video  delivery
that is now available.

     At  the  secondary  levels  we   consider   two   main
aspects which influence  the  goals  and  aims  of  math-
ematics   education:   the   (mathematical)   preparation
of students for their  lives  and  occupations,  and  the
role of mathematics  and  its  applications  in  society.
                                                     I
     The students' preparation  for  their  I'ves  and  oc-
cupations starts in the first  instance  at  school  with
its various disciplines.  Since  through  the  availabil-
ity  of  computers,  there  are  now  strong   tendencies
to introduce simulations  into  the  school  teaching  of
science, most  notably  in  biology,  or  of  introducing
elements of statistics and data analysis  into  the  mea-
suring   sciences   and   geography   (cf.    Winkelmann,
1987), this is obviously  a  challenge  to  the  teaching
of  mathematics:   Mathematics   should   elucidate   the
principles, possibilities and possible pitfalls of  these
methods;   ad-hoc-explanations   of   such   methods   by
the  specific  content-oriented  disciplines  are  surely
not  appropriate  for  giving  the  student  a   coherent
appreciation.

     It is  important  to  realize  that  routine  calcula-
tions of all complexities will be  done  increasingly  by
ubiquitously  available  machines  which  must  be   con-
trolled at various levels by the  users  concerned.  This
requires  more  insight,  more  breadth,   more   ability
to  check  consistency,  but  fewer  routine  algorithms.
Such an  emphasis  belongs  to  the  perennial  goals  of
mathematics  teaching,  of  course,  especially  in   the
new  math  movement.  But  now  there   is   really   the
possibility of leaving out  some  of  the  drill  because
technology can  take  over.  Even  an  insight  into  the
fundamentals  of  computers  and   their   programs   may
belong to the preparation for life.  This  can  often  be
shared  with  the  other  formal  discipline,   informat-
ics/computer science, if it is implemented.  It  is  hard
to be more  specific,  since  the  determination  of  the
elementary  and   more   advanced   cultural   techniques
which are  needed  by  the  future  citizens  presupposes
a futurist view of  society  which  is  notoriously  hard
to specify.

     As  to  preparation  for  vocations,   for   university
studies,  fundamental  ideas  and  experiences   in   al-
gebra,  geometry  and  fractals,  analysis,  data  analy-
sis  and  statistics,  simulation  and  chaos  would  now
seem to be  necessary  in  different  kinds  of  studies.
More specific  preparations  for  special  vocations  are
again  difficult   to   determine.   For   example,   CAD
(Computer-Aided  Design   which   helps   the   construc-
tion of planar, spatial and other  objects  on  the  com-
puter screen)  is  necessary  for  an  increasing  number
of technical vocations,  and  this  means  the  need  for
new  and  different  qualifications  in   geometry;   but
what is exactly  needed  and  how  to  build  a  curricu-
lum to fulfill the needs of the trades  remains  unclear.

The same is also  true  for  the  other  domains  men-
tioned in this chapter; therefore, it is not  laziness
that the descriptions above are  so  general  and  un-
specific. The general direction  of  necessary  change
can clearly be seen, but concrete decisions cannot  be
built on scientific knowledge yet; we have to  experi-
ment and gather ideas,  examples  and  proven  results
in concrete circumstances.
 
   Mathematics education at school not only   has
the task of delivering to students the  qualifications
asked for in vocations and daily life, but  it  should
also give insight into the role of mathematics in cul-
.ture and society, into the fundamental  possibilities
for understanding and  description  offered  by  math-
ematics,  and  into  connected  assumptions  and  lim-
itations. In this  respect,  on  the  one  hand  today
the greater part of the  applications  of  mathematics
is transmitted by  the  computer  and  thereby  influ-
enced in its character, as will be discussed  in  some
instance below, and on the  other  hand  the  computer
is  fundamentally  a  mathematical  machine  and  thus
its proliferation is a tremendous amplification of the
mathematization of our lives.
 

Primary School

     Computers and Calculators for Young
     Children

     The greatest  impact  of  computers  on  the  learn-
ing of school mathematics has  occurred  in  secondary
school. However, we wish to begin  by  discussing  the
primary school curriculum for three reasons:  .
o a natural and basically  positive  attitude  towards
computers can only be achieved at this level.
    Since primary school determines  a  student's  life-
     long  attitude  toward  mathematics,  we  must   use
     all possible means - and  the  computer  is  one  of
     the most powerful of these - to  create  a  positive
     attitude during primary education.
     it is necessary that teachers planning to use com-
     puters in secondary school  and  even  in  universi-
     ties understand what  was  done  in  primary  school
     and what the problems were there.
     The  first  major  need  to  socialise   with   peer
groups and to share them  arises  when  children  move
out of the  home  into  regular  contact  with  others
at playschool or infant school.  Here,  also,  serious
work starts in  developing  spoken  and  written  lan-
guage skills, learning about  the  world  and  meeting
basic processes  with  patterns  and  numbers.  Plenty
of play and creative  opportunities  are  provided  to
allow natural skills to flourish.
     How  can  technology  help  in  this   busy   active
happy  environment  of  early  childhood?   Technology
is certainly part of the world that  the  children  will
grow up in but one might feel it is not yet a part  that
children  need  to  meet  directly.  Indeed,  there  are
concerns expressed  in  some  countries  that  it  might
be positively harmful to allow  the  use  of  technology
before certain basic skills have been mastered.
     In the next section  we  shall  look  at  some  exam-
ples of  use  under  'content'  headings  although  they
also give rise to  cross-curricula  work.  For  ease  of
illustration  we  shall   take   Language   Development,
Early  Science  and  Basic  Mathematics  as   our   main
categories.  The  decision  not  to  limit  the  primary
school part of this article to  mathematics.is  deliber-
ate in view of the  fact  that  most  elementary  school
teachers carry a responsibility for the  major  part  of
a total  curriculum.  It  is  thus  important  that  the
use of  computers  be  set  in  this  context.  However,
the Language and  Science  examples  also  have  a  rel-
evance  to  mathematical  processes  although  this   is
not made explicit.
     Before looking at the specific examples, it  is  nec-
essary to discuss the  social  situation  that  children
find themselves in. Basically, there  is  a  teacher  to
whom  they  can  turn  and  who  organises   their   ac-
tivities during the day- there is a  group  of  children
that they work with, those  they  play  with  plus  spe-
cial friends that they confide in.  Thus  children  con-
tribute to a whole range of  interactions  sometimes  as
part of a large class, at other  times  with  a  smaller
group, often just to  one  other  person  and,  finally,
they must frequently work  things  out  as  an  individ-
ual. In short, the challenge that  young  children  face
of  being  a  member  of  the  classroom  community   is
complex and demanding.
     Children  need  to  develop  good  productive   rela-
tionships and for this they need  effective  verbal  and
nonverbal  skills.  Communication  through   body   lan-
guage and  other  nonverbal  signals  develop  naturally
and requires  no  formal  intervention.  With  the  spo-
ken and written word  the  structure  of  the  language,
although  not  formally  expressed,  begins  to  be  un-
consciously absorbed and then  actively  used  to  build
new  sentences  and  expressions.  This  somewhat   sur-
prising occurance indicates  the  importance  of  under-
lying  structures  as  an  aid  to  communication.   The
possible role  of  the  computer  in  this  process  was
mentioned above.
     We shall analyse, albeit  in  a  rather  crude  fash-
ion, the roles played  out  by  teachers,  children  and
computers in the examples that follow.
     Thus the focus of  the  following  descriptions  will
be  to  consider  the  quality  of   the   communication
in  the  classroom  community  and  to  identify  struc-
tures  and  roles  that  enhance  the  interactions  be-
they are.

     3. Using Key Handling Programs

     Programs such as  SEEK  can  be  used  in  a  surpris-
ing  number  of  ways  with  children.  Obviously   they
can be used to.identify things if  a  suitable  tree  of
questions' is already available. At the  other  extreme,
children can build their own tree  from  scratch,  given
a set of rocks, twigs or kitchen powders, for  instance.
     There are also  strategies  that  fall  between  these
two. If a class is planning to go  pond-dipping,  a  key
to  the  commonest  animals  might  be  created  in  ad-
vance,  using  information  from  books.   New   animals
can be added one at a  time  as  they  are  found,  pos-
sibly over a long period. This  may  well  be  the  best
approach with  large,  complex  groups  of  things.  The
initial skeleton tree can be designed so that  its  main
branches  represent  the  major  groups  (nymphs,   lar-
vae, snails, worms,  etc.)  and  the  research  involved
in creating it can give focus to the  childrens'  prepa-
rations for the first outing.
     In  the  classroom,   identification   exercises   can
provide very effective frameworks for  practice  of  ob-
servational  and  experimental  skills.  A  particularly
good  example  is  the   POWDER   tree   supplied   with
the  SEEK/THINK  package.   On   the   surface   it   is
simply  an  identification  key  for  common   household
powders, such as  sugar,  salt,  washing  powder,  flour
and  baking  powder.  The  questions,  though,  are  not
just  passive  observational  ones:  Most  of  them  ask
the  children  to  do  something  to  the   powder   and
watch its reaction.  In  the  next  column  is  part  of
the key as produced by SEEK on a printer.
     There is n6 one  way  of  classifying  things.  There
may  be  generally  accepted  ways   for   groups   like
plants, animals or rocks, but  even  these  are  subject
.to constant  argument  among  scientists.  If  children
are to understand why  things  are  classified  the  way
they are, they  need  to  explore  and  compare  differ-
ent ways. It is here that  programs  like  SEEK  display
their real value. By taking care of the  overall  organ-
isation of the tree, they let the  children  concentrate
on close observation, comparison  and  the  logical  and
language aspects of choosing good questions.
     Imagine that  a  group  of  children  are  trying  to
identify  some  epsom  salts  using  the  POWDER   tree.
They will probably find that it  is  wrongly  identified
as a salt. If  they  decide  to  extend  the  tree  they
wi 'll be asked to find  a  question  to  distinguish  the
two. This  is  no  small  challenge,  finding  the  best
question may take  a  lot  of  time,  experimenting  and
discussion. The first stage is to  find  out  everything
they  can  about  the  two  substances   by   observing,
 

   QUESTION                               YES              NO

I  Feel your powder?
   Is it smooth or
   floury?                                           2                3

2    Put some in a
     teaspoon and
     heat  over   a
     candle.  Can   you                    BAKING          4
     see lots of                                POWDER
     steam?

3    Look   through   a
     magnifying
     glass  to  see
     if it is lumps
     or crystals. Is
     it   crystals?                                   5                6

4    Put   a   drop of
      iodine on your                              FLOUR      ICING
      powder. Does it go                                         SUGAR
      blue/black?

5   Put some in a
     teaspoon and
     heat  over   a
     candle.  Does   it
     smell like                                    SUGAR               7
     toffee?

6    Put some in
     water and shake.
     Do  you  get  lots                        SOAP               POLY-
     of    bubbles?                                                      CELL

 7   Put   a   teaspoon
      of  powder  on   a
      saucer   and   add                      WASH-      SALT
      vinegar. Do you                         ING
      get bubbles?                              SODA

practical  testing  and  research  into  their  uses.  The
result may be quite a long list  of  differences,  so  the
second stage is to decide  on  the  best  question  to  be
added to,the tree.
     'Does it  dissolve  in  water?'  is  no  good  because
the both do.
     'Does it taste salty?' may  be  ruled  out  on  safety
grounds   (someone   may   try   to   identify   something
poisonous).
     'Do  you  buy  it  at  the  chemist?'  requires  prior

     knowledge  and  would  be  impossible  to  answer  if  yo
     really did not know what the powder was.

          'Does it have big crystals?' does  not  have  a  clea
     answer:  It  depends  what   you   compare   them   with.
     Also the crystal sizes of both vary enormously.

          'Does it have long, thin crystals?' is better, as  is
     'Does it turn into white  cake  when  you  heat  it  over
     a candle?'

          Some  of  these  problems  are   quite   subtle,   and
     children are unlikely to spot them  until  they  try  the
     'bad' questions in  a  complete  tree.  Fortunately,  all
     the  more  recent  programs  let  you  prune  and  repair
     a  tree  without  having  to  rewrite  the  whole  thing;
     so children  can  learn  from  their  mistakes  and  cor-
     rect  them  with  a  minimum  of  frustration.   A   good
     way of  identifying  problems  and  sharing  insights  is
     to encourage groups of  children  to  test  each  other's
     trees.
 
 

     4. Mathematics

     AUTOCALC   is   another    example    of    a    simple
program  that  promotes   considerable   discussion   and
sharing of processes.  It  enables  children  to  articu-
late  their  own  methods  and  ideas  and   has   proved
an extremely  valuable  way  to  build  their  confidence
in  their  mathematical  abilities.  The   children   are
challenged  by  the  program  to  try  out   their   men-
tal arithmetic skills  and  to  review  and  compare  the
range of possible processes. A  large  screen  is  needed
at the  front  of  the  classroom.  The  screen  presents
the problems in the following format:

                                   44
                              +   29
                                          ----

     After  a  delay  the  computer  then  supplies  the  an-
swer to the calculation
 

                                  44
                              +  29
                                  73

     The mode of the program is   to   generate   such
problems  by   selecting   random   numbers   according   to
the  parameters  set  at  the  beginning,  using  a   chosen
operation  and  displaying  the  answers  after   a   chosen
time  delay.  The  option  screen  used  for  defining   the
type of problem to be set is shown below:

          Type of problem            Subtraction

Difficulty Level                          Own
Top number                              1    to  20
Middle number                          1    to  10
Bottom number                         0    to  20
Delay time                                2 seconds

This option setting provides   simple    subtraction
 problems for young students.
     Imagine a class of  children  working  on  the  ways
in which they 'add  9'  to  numbers.  The  computer  is
set to produce problems  where  the  number  is  gener-
ated between 0 and 99, the second number  is  fixed  at
9 and the time delay of 3  seconds  before  the  answer
is given has been  set.  Fifteen  problems  appear  one
after the other and the children attempt  to  calculate
the answer before it  is  displayed  by  the  computer.
To  simulate  the  experience  complete  the  following
problems as quickly as  you  can:-

          28  90  32  77  88  79  37  66
          9+ -2+  9+  9+  9+  9+  9+  9+
 

     Probably after the first try at this task  the  chil-
dren will feel that they  might  be  able  to  get  the
answers in under  2  seconds  so  that  they  can  have
another  go  with  reduced  time  delay.   Some   might
even like to go at producing an  answer  in  I  second!
After this activity the children are asked to  say  ex-
actly how they got  the  answers.  The  following  list
of methods was the result of a class of ten  year  olds
sharing their ideas:

1.   Helen decided to add one to the 'tens' and then
     take one  away  from  the  'units'.
2.   Jonathan  was  happy  to  count  on  his  fingers  but
     didn't always bave time.
3.   Susan added 3 three times.
4.   Jo subtracted '1' and added '10'.
5.   Anne  worked  out  'how  many  to  the   next   10's'.
     This is then  subtracted  from  9  and  the  remainder
     added
     e.g.              78 + 9 = 80 + 7 = 87
6.   Simon added 2 four times, then 1.
7.   Jane  used   different   mathematics   for   different
     problems.
8.   Michael just  'knew'  the  answers!

The  children   greatly   enjoy   sharing   their   methods
and trying out  each  other's  ideas.  They  are  also  en-
couraged to use  calculators  -  various  tasks  are  given
  that begin  t-o  expand  their  understanding  of  num-
ber and to encourage  them  to  feel  confident  enough
to niove iiito estimating outcoining numbers  as  well.
AUTOCALC  can  be  run  in  a  mode  where  the  chal-
lenge is not to do the  calculation  but  to  spot  ev-
ery time an incorrect answer  is  displayed.  (This  is
called the 'oops'.mode.)  The  skills  needed  to  suc-
ceed here are now dependent  on  having  a  good  grasp
of nuniber  bonds  and  relationships.  Another  excel-
lent activity is to ask the  children  how  many  prob-
lems  they  can  make  combining   a   number   between
0-99  and  a  number  between  0-9  that  has  the  an-
swer of 5-1 e.g. 13 - 8 = 5; 1  x  5  =  5  etc.  After
exploring the problem in  groups,  the  children  offer
their  solution.  This  brings  out  some   fundamental
niathematical processes - classifying sets  within  the
solution set - setting the initial conditions in  order
to limit the solution set to  a  finite  set  and  many
others. The  children  express  these  ideas  in  their
own language and, of course, they  are  not  yet  aware
of the generalisation of  such  ideas.  However  it  is
at this point that we become  aware  that  this  simple
computer program has  given  the  children  a  stimulus
that  has  caused  them  to  become   true   mathemati-
cians. In  sharing  their  mathematical  processes  and
in valuing each other's ideas they will build  up  con-
fidence in their own abilities to  offer  something  to
the sub'ect. In this way we can  begin  to  remove  the
fear that so many people leave school  with  in  regard
to their mathematical abilities. A final stage  to  the
discussion of the '5's' problem is to  watch  the  com-
puter doing  the  same  problem  and  to  write  report
to 'Its parents' on its performance.  As  the  computer
applies an extremely simple algorithm  (it  Just  keeps
randomly  generating  problems  but   only   displaying
those that give the result of 5),  its  performance  is
certainly open to  criticism.  Here  are  some  of  the
children's reports:
 
 
 
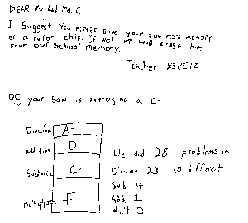
     Critics might say that  the  activities  promoted
with  AUTOCALC  are   not   valuable   because   they
are dealing with numbers out of context to  any  real
problem. However we  hope  that  the  examples  here,
which are only a minute part of the range  of  possi-
bilities, show children becoming aware of  their  own
power and thought processes and also  taking  over  a
range of 'teacher roles' at various stages.  Feedback
to the teacher of the children's  reasoning  and  the
way in which they articulate this is a major  contri-
bution of AUTOCALC.
     A few years ago Michael  Girting  (Her  Majesty's
Inspector) suggested that a definition  for  numeracy
might be 'appropriate use of an  electronic  calcula-
tor'. What number  sense  would  one  need  in  order
to qualify?
     We suggest:
1.   Instant command of single digit arithmetic
2.   Command of basic multiplication facts
3.   Skill in estimation
4.   Capacity to spot errors
5.   Capacity to select which  operations  are  appro-
     priate in any problem
     With the exception of  5  all  these  points  are
strengthened by the activities  possible  with  AUTO-
CALC.

     Concluding Remarks
     This section has taken just  a  few  examples  of
simple  software  to  illustrate  bow  computers  can
have a stimulating and refreshing  relationship  with
children. We  are  keen  that  the  computer  becomes
an accepted  assistant  and  friend  of  both  teach-
ers and children.The use  of  Logo,  data  banks  and
word  processing,  have  not  been  discussed   here   as
many books and  articles  are  available  to  the  reader
on  these  topics.  Such  languages   and   systems   can
be  employed  to  stimulate  discussion   and   exitement
such  as  is  described  here.  However,  they  can  make
considerable  demands  on  the   users   and   we   would
recommend  that  subsets  of  such   systems   are   used
to start with. Slow  progress  is  being  made  with  im-
plementing  a  curriculum  that  make  effective  use  of
computers and  calculators.  This  is  due  to  the  fact
that there is not as  yet  a  great  deal  of  curriculum
support materials to  introduce  the  range  of  learning
activities  that  simple  or  complex  computer  software
can  support.  However,  this  material  will   gradually
emerge  and  there  is  certainly  enough  available   to
any enterprising school  to  offer  children  the  advan-
tages of a computer in their classroom.
     Any  school  able  to  equip  each   classroom   with
a  single  microcomputer  would   gain   experience   and
confidence  within  a  matter  of  months   rather   than
years. Add to  this  provision  a  small  laboratory  for
word  processing  etc.  together  with  a   collaborative
staff exploring  possibilities  together  and  the  scene
will be set for an exiting time for children  in  such  a
school.

Secondary School

     Phenomena, Theories,
     Experimental Mathematics

     In  mathematical  knowledge  one  can   differentiate
between facts on  the  one  hand  and  the  insight  into
their  necessity  and  their  connections  on  the  other
hand,   or   between   phenomena   and   theories.   This
distinction  becomes  clear,  for  example,  in  the  do-
main of the  geometry  of  triangles:  Examples  of  phe-
nomena  are  the  observable  facts,  such  as  that  the
three  angel  bisectors  meet  in  one  point  and  simi-
larly for  the  perpendicular  bisectors,  that  the  sum
of the inner angles equals 180  degrees,  that  two  tri-
angles  which  have  the  two  sides  and  the   enclosed
angle  equal  have  all  other  measurable  parts  equal,
the formula  of  Pythagoras,  etc.  Most  classical  the-
orems  of  school  geometry  belong  here,  but  so  also
do  more  qualitative  facts  such  as ' : If two  sides  are
fixed in length, then the third side gets longer  if  the
enclosed angle  is  made  bigger  (up  to  180  degrees).
There  is  now  special  software  such  as  The  Geomet-
ric Supposer  or  Cabri  G6om@tre  which  helps  to  find
such  facts  by  giving  assistance  in  the  making  and
systematic variation of geometrical constructions.
     In the domain of theory  there  is  the  logical  or-
dering of facts (local  and  global),  the  insight  into
the  necessity  of  observed  facts,  the   determination
of the  proper  conditions  under  which  the  facts  re-
main true (the  domain  of  validity),  etc.  As  a  con-
crete example,  let  us  look  at  the  calculus  (analy-
sis).  Phenomena  are:  The  graphs  of  functions,   say
of f (x) = x sin llx, the fact that sin xlx  tends  to  I
as x tends to zero, the divisibility of x' - 1 by x  -  1
and the form  of  the  divisors,  the  formulas  for  the
derivatives of elementary  functions,  the  linearity  of
the integral, or the shape of  solutions  to  a  specific
initial value problem for a differential equation.
     To the domain of theories,  there  belongs  the  def-
inition and fundamental  properties  of  the  limit,  the
completeness of  the  real  numbers,  the  definition  of
the integral, the limits of  validity  of  theorems,  and
explanations of facts by arguments.
     It is interesting, that there may be  different  pos-
sible  theories,  for  example,  Euclidean  or  Cartesian
geometry,  with  formalist  or   constructivist   founda-
tions. Or, in the case  of  analysis  there  are  differ-
ent  possible  non-equivalent  theories,  the   classical
c  -  6-theory,  non-  standard  analysis  and  different
constructivist  approaches.  But  all   those   different
theories explain - in different  ways  -  the  same  phe-
nomena.  And  all  the  concrete  applications  of  geom-
etry or calculus only  rely  on  the  phenomena,  not  on
the  underlying  theories.  In  a  similar  wav,  comput-
ers  and  mathematical  software  work   exclusively   in
the  realm  of  the  phenomena;  they  can  only  exhibit
phenomena.  And  they  are  able  to  show  the   phenom-
ena even to  students  who  have  not  yet  mastered  the
theory.
     This is the  point  in  our  argument:  In  a  mathe-
matics  class  using  mathematical   software,   students
will get to see and  know  a  lot  of  mathematical  phe-
nomena.  The  mathematical  theory  then   has   to   ex-
plain  these  phenomena;  thus  mathematics   shifts   in
the direction of a science which  orders,  describes  and
makes  understandable  facts  that  are   already   known
and  obvious  even  without  explanation.  This   is   in
sharp contrast to  classical  teaching  methodology,  es-
pecially in such do.ziains  where  it  was  hard  to  ap-
proach  the  phenon-.,  la  without  theory  or  advanced
technology.
     Here  is  an  example.  In  the  study  of  functions
and  their  transformations,  traditional  teaching   de-
duced  behaviour  mostly  from  theory,  since  the   ac-
tual plotting of function graphs  by  hand  was  far  too
expensive, in terms of  time  and  labour,  in  order  to
make students see the  facts,  for  example,  the  graph-
ical  translations  connected  with  the   transformation
f (x) -* f (x + a). With the help  of  a  function  plot-
ter  they  may  observe  those   transformations,   first
connected  with  a  concrete  f  and  a,   then   system-
atically explored  with  free  chosen  examples,  and  in
between also formulated  as  hypothesis  and  verified
by arguments.  In  this  way,  the  temporal  order  0
phenomena and theories reverses, and  gets  closer  to
the usual habits of  mathematics  as  a  research  ac-
tivity. Of course, such an  approach  has  often  been
used  with  mathematical  content  where   exploration
of phenomena was cheaper.
     The didactical  paradigm  just  described  has  of-
ten  been  referred  to  as  "experimental   mathemat-
ics", but it has to-be stressed that theory  is  an  in-
dispensable part of it in  order  to  be  mathematics.
Just playing  around  with  a  function  plotter  does
not necessarily lead to  insight.  You  normally  need
hints, ideas, hypotheses, questions in  order  to  see
something and  get  involved.  (See  Goldenberg,  1988
for more specific  considerations  and  examples.)  As
a counterexample, using  fractal  generating  software
may give spectacular pictures of great esthetic  value
but, if you stop at the phenomena, you  won't  get  at
mathematics with such  software.  You  need  at  least
general concepts such as self-similarity or  symmetry,
which are also needed  for  the  better  understanding
and appreciation of the beauty  of  the  pictures  in-
volved.

     Software for Secondary School
     Mathematics

     We shall discuss this for three content areas
Geometry, Functions and Data Analysis.

          Geometry

     Two  software  packages   for   geometry   education
were   mentioned   above:   The   Geometric   Supposer
and  Cabri  Geometre  which  allow  constructions   of
most  of  the  problems  of  Euclidean  plane   geome-
try. A so-called draft mode allows the exploration  of
consequences of moving one point  in  a  figure  while
keeping its connections to other points (see Fig.  1).
Descriptions  and  examples  are  given  in   Schumann
[1990]. Here we shall describe two other pieces of
"teachware",  which   allow   some   unconventional   ac-
tivities which are  closely  related  to  the  curriculum
for grades 7 and 8.
 
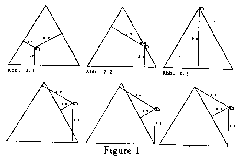
                                Fig.1
     The  elementary   didactical   philosophy   is   that
there  should  be  two  levels  of  action  in   geometry
classes,  when  using  a  computer:  On  one  level   the
pupils  should  learn  the  constructions  manually  with
ruler and  compass,  as  usual.  On  another  level  they
improve  their  competence   with   these   constructions
by  solving  geometrical  and   applied   problems   with
graphics  procedures  on  the  screen  which  they   per-
ceive  as  efficient  and  comfortable  tools.  In   par-
ticular, this use  of  computer  graphics  in  the  early
years of secondary school  has  proved  useful  in  three
modes:
l..  Using   procedures   for    ruler-and-compass    con-
     structions  which  have   already   been   understood
     as  building  blocks  for  more   complex   construc-
     tions without  the  need  to  repeat  the  elementary
     constructions again and again.
2.   Using   procedures   for   constructions   in    ways
     which  cannot  be  realized  with  ruler   and   com-
     pass.
3.   Using  procedures  for  large  and  technically  dif-
     ficult  constructions,  which  demand   many   itera-
     tions of elementary constructions.
     The  Geometric  Supposer  fits  in  mode  1.  We  now
discuss   two   other   software   packages,   SYMNLETRIC
TURTLES    and     KALEIDOSCOPE,     which     illustrate
modes 2 and 3.

     SYMMETRIC TURTLES (Graf, 1988)

     It is well known  that  Logo's  turtle  graphics  can
help  at  the  beginning  of  geometry  education.  As  a
tool  which  provides  an  extension  of  the  ruler  and
compass  a   "running   turtle"   has   been   developed.
This  follows  the  concept   of   Abelson's   dynaturtle
(Abelson  and  di  Sessa,  1985],  but   without   inertia.
To some extent  you  can  use  it  like  a  pencil,  con-
trolled with keys.
     Keys 1, 2 .. 9 put it in slow or faster  forward  mo-
tion on a straight line, key 0 stops it. Z or N lets  the
turtle  draw  or  not  draw  when  moving.  A,  S,  D,  F
effect small (5 degrees) or larger (15 degrees)  left  or
right turns of the stopped  or  moving  turtle.  Q  marks
the position of the  turtle  on  the  screen  and  deter-
mines  a  number  for  this  point.  This  point  can  be
reached again via keys K or P.  K  turns  the  turtle  in
its actual  position  heading  for  another  point.  This
corresponds  to  putting  a  ruler  through  two  points.
P  puts  the  turtle  on  an  already  marked  and  named
point. And so on.
     This  running  turtle  allows  construction  of  many
figures of  interest  in  plane  geometry.  Besides  this
than from the final picture. You see that  a  straight
line remains a straight line, you see how  the  direc-
tion changes under  axial  symmetry  and  how  it  re-
mains  the  same  under  central  symmetry.  You  also
see that a straight line and its picture are  parallel
under central  symmetry,  but  have  different  direc-
tions, etc. Figure 2 contains  some  examples.  Unfor-
tunately, the "dynamic" quality of  the  turtles  can-
not be seen from these figures.
 
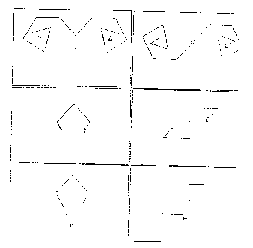
                                            Fig.2
     Figure 3  shows  how  the  following  question  can
be examined: "What  happens  when  reflecting  a  tri-
angle in different positions relative to the  axis  of
symmetry or a point?"
 
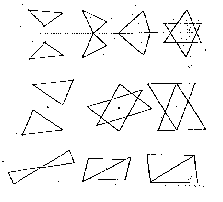
                                Fig.3
     Figure 4 gives a systematic  answer  to  the  ques-
tion, "How can  quadrilaterals  be  generated  by  re-
flecting triangles?"
 
                                            Fig.4
     First, it is convenient to choose a side of a  trian-
gle as an axis of symmetry.  Then  with  the  turtle  you
get a kite. The special case  of  an  isosceles  triangle
occurs if the angle adjacent to the axis is  90  degrees.
If this angle is greater than 90 degrees,  then  you  get
a  quadrilateral  which  is  not  convex.  You  can  also
get  a  rhombus  and  square  by  starting  with  special
triangles. But you  never  get  a  general  rectangle  or
a  parallelogram  or  a  trapezoid.  The   central   sym-
metry  turtle,  however,  applied  on  the  centre  of  a
side  of  a  triangle  produces  a  parallelogram   imme-
diately.  This  is  an  exciting  discovery.  The  choice
of this special point of reflection is suggested  by  the
experiments  shown  in  Figure  3.  Again,  no  trapezoid
occurs. This  fact  can  result  in  geometrical  discus-
sions. More  details  about  these  tools  are  given  in
Graf [1988].  Some  reactions  of  teachers  and  student
teachers to this  kind  of  teachware  and  some  experi-
ences in classes are also reported there.

     KALEIDOSCOPE

     In  a  paper  by  Graf  and  Hodgson  [1990]  it   is

look for the term. This is realized in  the  "Funktio-
nen raten" (looking for the formula) part in  Graphiz.
     For example, the  program  plots  the  graph  of  a
function - say f (x) = 2x - 3  -  but  does  not  show
the term (Fig. 10). The user has to make  use  of  the
information given in the  graph  to  guess  the  func-
tion term and  put  it  in.  The  computer  reacts  by
plotting (in another color, if  available)  the  graph
corresponding to the user's term  in  the  same  coor-
dinate system. If the user has  not  got  the  correct
solution (Fig. 11), he or she can  now  see  the  dif-
ference between the original  and  the  guessed  graph
and use this information to debug, that  is,  to  cor-
rect any mistake. As many  tries  as  desired  can  be
made. It is also possible to wipe out the screen  and
see only the original function.
 
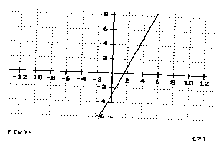
                                Fig.10

 
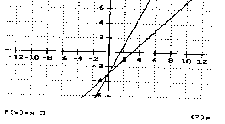
                            Fig.11

     The functions  plotted  by  the  program  are  of-
fered in difrerent sets, organized according to  dif-
ficulty and type of function (linear, quadratic,  cu-
bic, trigonometric, exponential, using absolute  val-
ues, etc.). The sets  can  be  changed  or  augmented
with a simple text editor by the  teacher,  according
to the needs of the  students.  A  specific  option  lets
the  program  be  used  by  two  partners   (individuals,
groups): the first gives  the  term  and  the  other  has
to guess it from its graph.
     The simple  idea  of  the  program  gains  its  moti-
vational  and  challenging  character  from  the  use  of
a  sophisticated  function  plotter,  which  comes  close
to  the  accustomed  appearance  of  terms  and   graphs,
and  from  its  deliberate  generosity  to  an  inexperi-
enced user.  It  is  simple  to  use.  The  user  is  not
penalized  for  wrong  answers.  And  it   has   adequate
error control, not  through  comparing  the  user's  term
with a predefined  list  of  possible  right  terms,  but
by  numerically  comparing  the  graphs  with  a  certain
tolerance. So the software  alms  really  to  help  users
to  evolve  and  debug  their  knowledge  about   elemen-
tary  functions  and  their   standard   transformations.
     The program is  to  be  used  mainly  by  individuals
or small groups, in a wide variety of  levels,  grades  7
to 12 and up. It may be  used  for  drill  and  practice,
and, of course, for remedial work.
 

          Data Analysis

     Statistical  education  -   as   mathematics   educa-
tion in general - often has  to  cope  with  the  problem
that, in order to  solve  real  problems,  the  necessary
techniques are  taught  and,  in  consequence,  also  un-
derstood by students  in  isolation;  their  proper  con-
ditions of application, their region of  validity,  their
limits  are  perhaps  theoretically  known,  but   seldom
part of active  knowledge.  In  order  to  overcome  such
limited  understanding,  one  method   is   to   confront
students  with  problems  connected  to  themselves,   so
that  they  don't  take  the  methods  as  neutral,   but
of real  importance.  One  of  the  goals  of  the  soft-
ware Times is just  to  give  students  some  real  data,
connected to themselves,  in  order  to  analyze  and  to
draw  conclusions  from  the  data  and   thereby   about
themselves.
     The  software  allows   experiments   with   reaction
times:  The  computer  produces  a  specific  signal  and
one of the students has  to  react  in  a  specific  way,
for example, by pressing  a  specified  button,  and  the
computer  measures  ttie  reaction  time.   The   process
repeats, and the data are  stored  into  a  file  bearing
the  name  of  the  student.  Another  student  does  the
same  procedure,  and  the  data   is   compared.   Which
student is better? Is the  arithmetical  average  a  fair
arbiter  or  is  the  median  better?  How   should   one
judge  extreme  values?  The   program   offers   several
methods  of   comparing   data,   including   some   well
known  statistical  techniques.  It  calculates   diverse
quantities such  as  averages,  variances,  the  plot  of
one distribution of values  against  the  other  It  doe
QQ-plots, displays  the  data  as  time  series,  etc.  In
defending their results,  the  students  hopefully  learn
to judge cautiously, to see  the  techniques  as  helpful
but normally not decisive tools,  and  the  necessity  of
properly  interpreting  the  data  rather  than  automat-
ically drawing  conclusions  after  a  routinely  applied
test.

     General Tools and Methods

     Besides studying  softwarf!  for  specific  mathemat-
ical areas like the ones just discussed, it is  important
to  consider  software  which  supports  specific  mathe-
matical  methods  which  have  importance  in   different
areas. Here algorithms in  their  original  sense  (think
of  Euclid's  algorithm)  are  most  familiar  and   were
integrated  into  mathematics   education   even   before
the advent of  computer  systems.  First  we  shall  give
an example of  an  algorithmic  strand,  which  fits  the
curriculum   for    the    German    "Gymnasium".    From
this you will be able  to  see  how  this  old  mathemat-
ical  idea  of  algorithm  can  be  extended  to  a  num-
ber   of   complex   mathematical   problems.   Then   we
shall  discuss  the  general  problem  of  how  to   com-
bine  in  class  teaching  students  to  understand   and
execute  mathematical  methods   and   to   solve   math-
ematical  problems  (from  multiplication   to   integra-
tion) by hand  or  brain  with  the  need  to  tell  them
that there  are  computers  which  can  do  these  things
easi 'ly if you  just  give  the  problem  to  them  in  the
proper  way.  This  is  the  black  box/white  box  prob-
lem.  Finally,  we  discuss  two  more  general   methods
of  growing  importance  in  mathematics  education   (as
well  as  in  mathematics  research)  -  simulation   and
model building.

          The algorithmic strand.

     Algorithms  are  patterns  with  a  certain   schematic
background;   although   high   mathematical    invention
was  necessary  for  their  discovery,  only  stupid  and
exact  processing  is  needed  for   their   application.
With  this  didactic  philosophy  the  teaching  of  con-
cepts  and  theories  of  mathematics  had  priority   at
schools. The use  of  algorithms  formed  the  center  of
exercises,  homework  and  control  of  achievement   and
so pupils were educated  as  if  they  were  little  com-
puters. Related to  this  secondary  role  of  algorithms
is the fact that several thousand  years  of  history  of
mathematics  have  not  produced   a   uniform   language
for  the  description  of  algorithms.  Now  there  is  a
continuous algorithmic strand  which  forms  15%  of
the curriculum in mathematics education  during  the
nine years  of  German  grammar  school.  (We  begin
at year five since we do not consider the four years of
primary education.) The following list shows typical
algorithms and also their related subjects.
5    Relations  between  the   fundamental   arithmetical
     operations
     Transformation  between   numbers   with   different
     bases: (10,2,5,16 etc.)
     Division algorithm
     Sieve of Eratosthenes
     Optimizing terms
     Summation  of  arithmetical  series   according   to
     Gauss
     Fundamental operations with sets

6    Calculation with fractions (handling formal
     rules)
     Greatest   common   divisor   and    least    common
     multiple (algorithm  of  Euclid  in  several  varia-
     tions)
     Prime  numbers,  twins  of  prime  numbers,  distri-
     bution of prime numbers etc., factor'sat'on of
     numbers
     Arithmetic means, relative frequencies
     Diagrams of descriptive statistics

7    Tables of proportions
     Calculation of percents and interest
     Random experiments
     Constructive geometry in two dimensions
     Geometrical mapping

8    Algorithm of Heron
     Iterations for linear equations
     Symbolic processing with equations

9    Solution of quadratic equations
     Graphs of quadratic functions
     Combinatorics
     Continuation of geometry (similarity)

10   Several methods of integration of the circle
     Division of polynomials
     Trigonometric construction
     Descriptive statistics

11   Experiments with sequences and series
     Discussions of functions
     Algorithm of Newton with variations
     Regula falsi
     Methods of optimisation

12   Methods  of  integration   according   to   Simpson,
     Gauss, Romberg etc.
     Symbolic integration
     Algorithm of  Gauss  for  systems  of  linear  equa-
     tions with variations
     operations with matrices etc.

13   Stochastic simulations
     Symbolic handling of limits (I'Hospital)
     Standard methods of inductive statistics
     Methods  for  numerical,  graphical   and   symbolic
     solution of simple ordinary  differential  equations
     This listing refers to a basic level of  higher  ed-
ucation.  For  the  advanced   level   ("Leistungskurs"
with 6 lessons in the week) a lot of possibilities  can
be added in the last three years such as:

     complex   numbers,   special   numerical    methods,
     algorithms of  the  theory  of  graphs,  fitting  of
     curves  according  to  Taylor  and  Gauss,  interpo-
     lation  of  functions  according  to  Lagrange   and
     Newton, cubic  splines,  study  of  nonlinear  iter-
     ations, mapping  and  representation  in  three  di-
     mensions,   constructive   non-euclidean    geometry
     etc.

     Also in the content of an  algorithmic  strand,  the
methodological  aspects  need  not  be  lost.   Several
basic formulations of  computer  algorithms  are  help-
ful  for  mathematical  comprehension,  too.  For   ex-
ample, pupils always  have  difficulties  understanding
the usual notations of  sums,  double  sums,  etc.  The
algorithmic notation using for-loops  or  nested  loops
removes many difficulties  in  understanding  the  role
of  summation  index  etc.  The  practice  of  program-
ming recursions is helpful for understanding  the  log-
ic'al basis of induction proofs, etc.
       For nearly all of the subjects  listed  software  is
available, some  of  it  with  more  options  than  are
needed in  schools.  Most  teachers  are  pleased  that
they do not have to  enter  into  the  specialities  of
graphic representation  and  the  other  "higher"  work
of computer  insiders.  Still  some  of  them  remember
another 'kind of work only a few  years  ago:  For  im-
portant  algorithms  of  mathematics  (Euclid,   Gauss,
Newton,  Simpson  etc.),  teachers  themselves  had  to
write  their  own  programs.  The  advantage  of  this
was that they could develop the  central  ideas  simul-
taneously in their classes and  in  the  programs.  The
disadvantage  was  that  the  handling  of  many   pro-
grams was not easy.  Still,  a  further  advantage  was
that  the  teacher  could  modify  an  algorithm  using
the (sometimes  unusual)  suggestions  of  the  pupils.
As  an  example,  in  Newton's  method  for  the  solu-
tion of transcendental equations, you  could  take  the
tangent of a function instead of the  function  itself.
Or you could  take  tangents  with  the  same  constant
slope as the first tangent  (the  method  converges  in
many cases). Alterations of  this  kind  are  generally
impossible  with  acquired   programs,   which   seldom
allow  such  open  didactical  processing.   Naturally,
for these purposes  the  teacher  needs  a  simple  and
transparent  computer  language   with   natural   key-
words and sufficient  mathematical  operators  as  well
as  a  compiler  which  can  understand  the   language
in  the  same  sense  as  humans.  Teachers   need   as
well  a  good  cooperation  with  teachers  and  pupils
of  computer  science,  who  can  construct  good  pro-
grams according to  their  desires.  Some  programs  in
the school market need  to  have  a  didactical  dimen-
sion so that, for example, the  plotting  of  functions
can be stopped and continued  using  the  intuition  of
the pupils.  During  algorthmic  processing  intermedi-
ate suppositions about the results should  be  possible
which can be verified or falsified.

     Symbolic Processing/Symbolic
     Manipulation

     In recent  years  symbolic  processing  for  personal
computers has  entered  into  schools  (see  the  chap-
ter  by  Hodgson  and  Muller).  Solving   linear   and
quadratic equations,  equations  of  third  and  fourth
degree, large systems of linear equations,  simplifica-
tion of rational expressions with  "towers"  of  double
fractions, division and simplification  of  polynomials
can all be done  with  symbolic  algebra,  often  inte-
grated with the direct processing  of  very  large  in-
tegers.  Where  exact  methods   fall,   approximations
are possible.  Symbolic  differentiation  and  integra-
tion, symbolic vector analysis and, finally,  the  sym-
bolic solution of ordinary  differential  equations  of
first and second order  together  allow  the  possibil-
ity of ignoring all the  rules  of  school  mathematics
in a traditional sense.  These  packages  are  made  by
professionals. Therefore, they  often  do  not  present
intermediate  steps  and  some  other  didactical   re-
main. Some  of  the  symbolic  packages  are  not  pro-
grammable  by  the  user.  Nevertheless  the  union  of
numerical, graphical and  symbolical  tools  has  enor-
mous power for schools.

     Enlightenment through Black Boxes

     In  a  recent  article,  Buchberger   (1990)   asks,
"Should  students  learn  integration  rules?",   given
that now  there  are  computer  algebra  software  sys-
tems available  which  solve  any  integration  problem
much more quickly  and  more  reliably  than  any  stu-
dent  could  ever  do  with  paper  and  pencil.  Buch-
berger immediately generalizes  the  question  for  all
those  areas  of  mathematics  which  are   "trivialized"
by   modern   software,   especially   computer   algebra
systems.  He  answers  -   for   mathematics   and   com-
puter science majors  -  with  his  "White  Box  /  Black
Box - Principle":  Students  should  learn  the  theories
and algorithms of such an area  first,  using  the  soft-
ware only for subordinate tasks  (e.g.  partial  fraction
decomposition)  but,  after  having  studied  the   area,
all calculations from this area should  be  left  to  the
computer.
     For  schools  and   general   mathematical   software
the  situation  is  more   complicated:   Numerical   and
graphical oriented software doesn't  trivialize  an  area
of  mathematics,  but  may  provide  profound   help   in
solving  problems;  school  mathematics  does  not   only
provide  mathematical  theories  and   algorithms   but
also their intended  applications,  their  modes  of  use
and  the  translation  schemes  needed  in   using   them
outside  of  pure  mathematics.  High   school   students
are  just  not  future  mathematicians,  but   could   be
regarded  as  future  users  of  mathematics   as   well,
who  obviously  should  have  a  different  attitude  to-
wards mathematical tools.  So  here  we  do  not  give  a
recipe  but  rather  some  considerations   which   might
help in coping  at  school  level  with  the  problem  of
using  ready  made  software   which   cannot   be   made
"translucent",  since  the  details  may  be   too   com-
plex, or totally  hidden  from  the  user,  or  just  not
worthwhile  studying  for  secondary   school   students.
     First of  all,  using  ready-made  mathematics,  even
if not fully understood, is to be seen as taking part  in
mathematics as a social  enterprise.  It  may  be  looked
on as  part  of  teamwork:  Users  rely  on  professional
mathematicians   and   programmers.   But    the    coop-
eration  is  anonymous  since  the  user  can't  talk  to
"coworkers", and users  have  to  know  a  lot  in  order
to use  the  black  box  correctly  and  with  beneficial
results.  But  knowledge  about   black   boxes   (proce-
dures, algorithms, etc.) can be of various kinds:
     Logical  or  erternal  The  user  knows   the   math-
ematical specification of the  result  the  software  de-
livers, but doesn't know  the  method  by  which  it  has
been achieved.  This  is  the  classical  black  box  and
is usually the case with  the  use  of  computer  algebra
systems  or  simple  calculators.  A  symbolic   integra-
tion  can  be  understood  (and  independently   checked)
even   if the internal Risch  algorithm  isn't  understood
or its existence even  known.  The  cosine  of  a  number
can be  interpreted  correctly  as  the  best  approxima-
tion  within  the  domain  of  machine  numbers  to   the
correct real number, etc.

     Analogous. If a complete  specification  of  the  re-
sult of the  software  is  not  available,  an  analogous
knowledge  of  a  similar  algorithm  may   often   help.

The graph of a function, as  displayed  by  a  function
plotter, is different from the graph  of  the  function
as  normally  defined  within  mathematics.   But   the
experience of doing function  plotting  and  a  reflec-
tion on the possible  pitfalls  (e.g.  vertical  asymp-
totes,  discontinuities  or  the  proper  determination
of  m&xima)  may  help  in  understanding  results  and
becoming aware of possible limitations.  For  the  nor-
mal student it is not worthwhile to learn  the  special
tricks and algorithms  programmers  of  function  plot-
ters use to give reasonable results even  in  difficult
situations.  Analogous  knowledge  is  needed  in  gen-
eral in the use of numerical software -  possible  pit-
falir,, trade-offs between step widths  and  obtainable
accuracies, between reliability and speed, etc.
     Algorithmic. Here  the  user  knows  -  on  a  cer-
tain level - the  specific  algorithmic  approach  used
by the software, for example, that  the  numerical  in-
tegration  software  uses  Simpson's  rule,  which  the
use had applied in  some  hand  calculations.  But  for
a suitable use of the software, the user  has  to  have
some  more  general  knowledge,  too  -  the   approxi-
mation character and the order of  the  algorithm,  its
domain of validity, in  what  circumstances  to  switch
to other algorithms, etc.
     All three kinds of  knowledge  have  their  special
value, and  in  most  circumstances  they  should  com-
plement each other. There is no a priori  best  way  of
enlightening a software black  box.  Of  course,  math-
ematics  teaching  has  the  duty  to  enlighten  black
boxes, to  make  them  grey  at  least,  but  in  which
way and to what extent has to be  decided  in  view  of
the intended use of the software, the  kind  of  knowl-
edge to  which  this  new  knowledge  is  to  be  added
and connected, and  to  the  overall  goals  of  mathe-
matics teaching in the specific age  group  and  school
system in particular.

     On the Concept and Importance of
     Simulations

     How  does  one  simulate   a   dynamical   process?
Such a process is described by specifying  the  transi-
tion from one state of the system to the "next"  state;
mathematically this is done  by  (systems  of)  differ-
ence or differential equations. In  order  to  simulate
such a process, one first has  to  specify  all  param-
eters, initial states and possible external  influences
numerically, and  then  follow  the  evolution  of  the
states numerically, replacing  all  mathematical  oper-
ations which have no  direct  arithmetical  translation
by  numerical  approximations.   Some   ending   condi-
tions have to be efficiently specified, too, for  exam-
ple, the maximum number  of  states  to  calculate,  in
order to prevent never ending calculations.

     The  resulting  numbers  -  normally  quite  a  lot   -
can be given as  tables  or  graphics.  If  the  concrete
choice of parameter  values  or  initial  states  is  not
dictated by the  situation  but  just  ad  hoc  in  order
to be  able  to  start  the  simulation  run,  the  whole
process will  have  to  be  repeated  with  other  values
fixed  -  that  means  defining  another  scenario  -  to
get an overview oyer  the  behaviour  of  the  system  in
a range of scenarios.
     From  this  description  we  have  a   geberal   infor-
mal  definition:  By  simulation  (in   mathematics)   we
understand  the  effective  operational  translation   of
mathematical  objects   or   processes   into   numerical
operations.  (Outside   mathematics   the   concept   has
to be extended, to include  the  building  of  a  mathe-
matical model first.)
     Simulation  in  this  sense  is  a  general   mathemat-
ical  method  which  has  always  been   used   but   has
gained   importance   enormously   through   the   avail-
abilty  of  effective  numerical   machines,   especially
computers.  As  a  method  it  is  very  often  not  dif-
ficult to apply, and  it  can  be  a  mighty  instrument,
especially  if  combined  with  other,  more  traditional
mathematical  methods  such   as   proof,   construction,
algebraic calculation, analysis, etc.
          Here are some examples of simulations:
     o  Function  plotting.  The  mathematical  object   is
the graph of the function, say of f (x) =  sin  x,  which
is a subset of R'.  For  the  simulation  one  has  first
to fix boundaries, say from -7r  to  27r,  then  approxi-
mate the interval [-7r, 27r] by a finite set of  floating
point numbers,  calculate  approximations  to  the  sine.
of these  numbers,  determine  screen  pixels  to  corre-
spond to the  calculated  values,  connect  those  pixels
by the  built-in  "line-drawing"  routines,  and  display
the  result.  The  filing  of  parameters   will   become
even  more  apparent,  if  you  simulate  functions  with
parameters, say f (x) = sin(ax), a E R.
     o  Stochastic   simulation.   The   mathematical   ob-
ject is, for example,  a  stochastic  variable  with  its
distribution,  mean  and  variance,   say   a   uniformly
distributed  variable   transformed   by   some   compli-
cated process or function f. To  simulate  it,  you  take
a  finite  number  of  uniformly   distributed   (pseudo-
)random  numbers,  transform   them   by   (a   numerical
approximation to)  f,  take  the  resulting  finite  dis-
tribution  as  an  approximation   to   the   distribution
sought, and calculate its mean and variance.
     o Solution to a differential equation.  The     math-
ematical object is the  general  solution  to  the  given
differential  equation.  To  simulate  it,  one   chooses
several different initial conditions, solves the  result-
ing initial  value  problems  by  numerical  methods  and
plots the  results.  The  emerging  picture  should  give
some insights into the  flow-lines  of  the  differential
equation,  its  overall  behaviour  and  possible   loca-
tions of critical points.
     Simulations  normally   share   a   double   experimen-
tal  character:  First  by   the   numerical   approxima-
tions whose  errors  can  be  only  estimated  since  the
assumptions of strict error control in  most  cases  can-
not be verified by  numerical  methods  alone,  and  sec-
ond by the fixing of  the  parameters,  boundaries,  etc.
Simulations  need  to  be  complemented  by   some   the-
ory, however rudimentary, in order  to  lead  to  insight
and  understanding.  Thus  the  plotting  of  the   sine-
function  can  only  give  a  non-misleading   intuition,
if the  continuity  and  periodicity  are  known  or  can
be abstracted by  the  consideration  of  a  well  chosen
sequence  of  (simulated)  pictures   with   some   zoom-
ing  or  similar  means.  The  insight  does   not   come
from the pictures. The  intellect  of  the  students  has
to see the  connections  between  the  pictures  and  the
necessities behind them;  but  to  see  the  facts  given
by the  simulation  may  strongly  help  the  student  to
understand the facts given by some theory.

     Model Building

     The  building   of   mathematical   models   is   seen
by  many  people  as  the  heart  of   application   ori-
ented  mathematics  teaching.  If  done   properly,   the
usual restriction  to  linearity  assumptions  will  soon
be noticed as  inappropriate,  and  the  use  of  simula-
tion software in  order  to  explore  the  (mathematical)
models developed becomes necessary.
     Here  we  describe  briefly   dynamic   model   build-
ing  of  simple  growth  processes  in  the   mathematics
classroom  with  the  program   Modus,   which   at   the
moment is  being  tested  in  schools  in  a  preliminary
version.  As  with  most  dynamic  modelling  tools,  the
crucial concepts are the distinction of  the  main  vari-
ables as levels and flows. Levels  can  only  be  changed
through flows;  this  property  is  described  in  formal
mathematical language by use  of  difference  or  differ-
ential equations, the  flows  being  the  derivatives  of
the levels. The model  building  is  done  by  construct-
ing  structure  diagrams,  thus  avoiding  the  necessity
for  an  abstract  formal  language.  The  students  eas-
ily develop linear  and  exponential  models  of  growth.
The step  from  linear  to  exponential  growth  is  made
by changing the constant  flow  to  a  (linear)  function
depending on  the  level,  thereby  introducing  a  first
feedback loop (see Fig. 12 and 13).
 
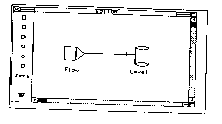
                                Fig.12

 
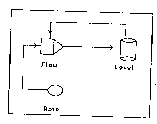
                        Fig.13

     Students soon detect that  exponential  growth  is
possible - and widespread -  only  in  the  beginning
phases of growth processes, be it  population  growth
in a new environment, growth of  individuals,  devel-
opment of first love, spread of rumors and epidemics,
but growth eventually has  to  slow  down.  In  model
building, this is interpreted as a dependency of  the
growth rate on the level reached,  thereby  introduc-
ing a new feedback loop, now negative,  which  yields
logistic growth (Fig. 14). Even without  ariy  formu-
 
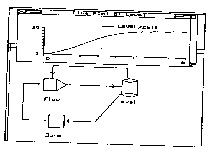
                        Fig.14

las for the logistic function, the growth behaviour
can be completely understood from the model itself,
and becomes evident by observing parts of the phase
diagram being generated dynamically (Fig. 15).
 
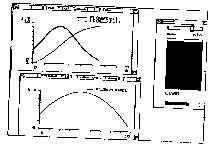
                             Fig.15

     Students (grade 10 or higher) learn to use the  ar-
gument that from  the  model,  the  concrete  quadratic
dependency of the flow on the level is clear.  A  posi-
tive flow causes the level to grow, which means  a  mo-
tion in the phase diagram to  the  right,  now  causing
a new flow,  etc.  The  motion  in  the  phase  diagram
slows  down  and  eventually  (virtually)  stops,  when
the flow approaches zero. So  the  equilibrium  can  be
determined  from  the  model,  and  similar   arguments
with starting points above equilibrium  show  the  sta-
bility property.  Such  qualitative  understanding  has
to be developed carefully since it  is  not  easy,  but
it  is  more  adequate  than  reasoning  with  formulas
which  immediately  break  down  when  the   model   is
further refined.

Conclusion

     Consequences for Organisation and
     Curriculum

     Organisation problems related to the  use  of  com-
puters in schools have  been  solved  only  for  demon-
stration  lessons  by  teachers.  Overhead   projectors
with transparencies for all explications and a  special
overhead display  for  all  output  from  the  computer
instead of the blackboard are  standard  in  many  Ger-
man schools. But 10  terminals  are  not  enough,  par-
ticularly if students  of  informatics  classes  occupy
the stations for many  hours.  Supervision  cannot  al-
ways  be  done  by  teachers.  The  ordinary   homework
of pupils of math classes using  the  computer  is  too
easily pushed aside;  only  pupils  with  computers  at
home can help theirselves, provided that  their  equip-
ment is  hardware  and  software  compatible  with  the
equipment of the school. It is difficult too, to  orga-
nize access to 10 terminals durin  a written
25 pupils in  the  class.  Therefore,  often  theoretical
questions  related  to  algorithms  (additional   special
cases, restrictions, possibilities for application  etc.)
have to substitute for the real  use  of  the  algorithms
for problemsolving in examination periods.
     The  consequences  for   the   curriculum   are   very
important.  School   mathematics   was   determined   for
centuries  by  the  number  of  accessible  methods   for
.solving  problems  -  equations  of  no  higher   degree
than  2,  systems  of  equations  with  3x3  or  4x4  ma-
trices etc.  Application  problems  were  selected  care-
fully so  that  powerful  computational  tools  were  not
needed.  With  the  speed  and  the  capacity   of   mem-
ory  of  modern  computers  in   schools   (newer   stan-
dard:   8.0386   processors,   1.2   MB   RAM),   numeri-
cal  and  graphical  approximations  for  solving   equa-
tions of  higher  degree  and  handling  matrices  of  10
or  20  columns  and  rows  are   no   problem.   Graphi-
cal representation of  large  sets  of  higher  functions
or of complicated  geometrical  situations  are  also  no
problem  as  are  the  symbolic  transformation  of  com-
plicated rational  terms  or  the  symbolic  solution  of
differential equations with  interesting  initial  condi-
tions. With these tools  teachers  can  leave  the  small
garden  of  traditional  school  problems   and   amplify
enormously  the  orientation   to   modern   application.
     Let   us   demonstrate   this   with   two   examples.
First,  from  pure  mathematics:  After  teaching   curve
fitting  by  Taylor  approximations  or  Fourier  approx-
imations  in  the  classical  manner  with.   the   usual
demonstrations  you  can  continue  with   Pad6   approx-
imations using rational  functions  and  use  these  for.
good  approximations  to  functions  with   singularities
(see Fig. 16).
     Our  second  example   is   from   applied   mathemat-
ics:  The  teacher  can   show   how   to   compute   ap-
proximations to  curves  of  highways  in  the  student's
neighbourhood  by  parametric  splines  with   the   help
of the computers.
     Thus various  new  fields  are  opened  for  the  cur-
riculum.  Simulations  in  natural  science  and   social
science using systems  of  difference  equations  can  be
used -to solve  interes'ting  environmental  or  economic
problems  never  before  accessible   in   schools.   The
theory  of  graphs  or  the  theory  of  functions   with
complex  variables  are  other  examples  of   new   ele-
mentary work with modern tools.

     Speculation on the Future

     During  the  first  twenty  years  of   computer   use
in schools,  the  mathematics  classroom  was  the  first
place  where  most  students  met  a  computer  at   all.
So math  teachers  had  to  pursue  an  additional  goal:
 
                        Fig.16

Make students familiar with  the  basic  structure  and
function of  a  computer  system  and  teach  them  how
to manipulate it. This situation  has  changed  rapidly
and will have changed totally in the near future  since
most  students  now  get  acquainted   with   computers
in their daily lives, in their family and  recreational
environments,  perhaps  in  computer   science   educa-
tion,  and  so  on.  This  means  the  computer  has  a
new  importance  in  math  education,  a  more   fruit-
ful  one,  more  oriented  towards  mathematics.   This
is described as  follows  in  a  study  of  mathematics
education  for  the  information  age  to  be  realized
in  the  Japanese  New  Mathematics   Curriculum   [Fu-
jita/Terada 1991]. In  upper  secondary  schools  pri-
ority should be

     "on giving to  students  opportunities  to  do
     mathematics   rather   than   improving   their
     techniques.  Students  should  understand  that
     computers are powerful tools  for  intellectual
     activities by human  beings.  In  this  connec-
     tion, studying mathematics  may  be  the  first
     as well as the best experience for students  to
     use computers for  properly  intellectual  pur-
     poses,  namely,  to  study  academic   subjects
     with   computers.   These    experiences    could
     even be regarded as a prototype  of  scientific
     research activities with computers.             Some
     good students will  have  chances  to  observe,
     to  model  and  to  analyze  in  a   mathemati-
     cal  manner  various  phenomena  presented   by
     computers.   Furthermore,   computer    simula-
     tion is close to mathematical reality.  On  the
     other  hand,  computers  are  extremely   help-
     ful in fostering students' mathematical  liter-
     acy.  Rich  mathematical  experiences   offered
     by computers, particularly  those  through  op-
     erational work by students, will pave  the  way
     for the majority  of  students  to  grasp  con-
     cepts  and  to  understand  fundamental   facts
     in mathematics."

     The New Curri,culum plans  three  courses,  Math-
ematics I - 111, in grades 11 - 13 with a total of  10
units (1 unit requires 35 ciass hours  of  50  minutes
each), covering a core of mathematics  to  be  learned
by all students with Math III certainly to be  learned
by all science and  technology  students,  Three  more
courses, Mathematics A, B, C, in grades 11 -  13,  to-
talling 6 units, are composed of four  option  modules
from which two  modules  are  freely  chosen  for  in-
struction by teachers or schools.  Module  4  of  Math
A, computation  and  computers,  offers  students  the
chance  to  get  to  know  and  become  familiar  with
computers as a  tool  for  mathematics.  Module  4  of
Math B,  algorithms  and  computers,  deals  with  the
powerful function  of  computers  in  doing  algorith-
mic computations  in  mathematics.  Math  C  is  char-
acterized by  the  key  phrases  "application  minded"
and "do math with  computers"  in  the  areas  of  ma-
trices and linear computation,  various  curves,  con-
ics  and  polar  coordinates,  numerical   computation
and statistical processing. The  study  mentions  that
the newly introduced topics related  to  computers  in
Japanese  high  school  mathematics  require   certain
preparation  for  success,  namely,  purposeful  text-
books, effective teacher  training,  quality  software
and relevant development  of  teaching  materials  and
methods.  Indeed,  the  educational  use  of   comput-
ers in class is non-routine and  should  b.e  explored
wi 'th respective emphasis  of  its  three  aspects;  the
teacher-initiated  use,  the  student-initiated   use   and
the system-initiated use.
     From   the   viewpoint    of    a    computer-supported
curriculum,  teaching  with  computers   in   a   classroom
will consist of the following six components:
1)    "trial', where learners are invited to the new
     topic  with  fun  applications  offered  by  the  corn-
     puter.

2)   "approach",   where   learners   have   heuristic   and
     operational  experiences  with  the  aid   of   comput-
     ers.

3)   "teaching",  where  the   teachers   give   a   lecture
     and  learners  get   supplementary   review   and   as-
     sistance from computers.

4)   "experimental    understanding",     where     learners
     grasp  concepts  and  facts   through   inductive   and
     experimental  recognition  with  the  aid  of   comput-
     ers  without  being  burdened  by   too   much   drill.

5)   "exercise",  where  learners   can   perform   adequate
     exercises  at  their  level  and  using  standard  (but
     interactive) CAI.

6)   "survey",  where  learners  review  the   topic   which
     they  have  learned  and  are  given  chances  to  view
     further developments and applications,

     The   principal   underlying   purpose   of   the   New
Japanese   Curriculum   is   to   cultivate   "mathematical
intelligence'  by  aiming   at   two   targets:   M@themat-
ical  Literacy   and   Mathematical   Thinking.   The   as-
pects   from   the   curriculum   mentioned   above    show
that  computer  systems   are   considered   to   be   very
helpful for both fields.
     These  two  fields  are  also   mentioned   among   the
principles  for  the  development  of  a  new   mathematics
curriculum  in  the  USA  by  2000   [Ralston   1990].   In
this reference  it  is  stated  that  "Mathematical  educa-
tion  should  focus  on  the   development   of   mathemat-
ical  power  not  mathematical  skins".  As   to   informa-
tion  technology  there  is  this  principle:  "Calculators
and  Computers  should  be   used   throughout   the   K-12
mathematics    curriculum;    moreover,    new    curricula
and  new  curriculum  materials  should  be   designed   in
the  expectation  of  continuous  change   resulting   from
further   scientific   and   technological   developments".
Goals from these  principles   follow   for   the   elemen-
tary grades (1-6) as  well  as  for  the  secondary  grades
(7-12).  So "the   teaching   of   arithmetic   in   elemen-
tary schools should be characterized by :...      a      use
of  computer  software  in  the   teaching   and   learning
process, ... proper  and  efficient   use   of   calculators
for most  multi-digit  calculations  as  well  as  calcula-
tions  involving  negative  numbers,  fractions  and   dec-
imals".   One   important   example   of    computer    use
in  the  secondary  curriculum  follows   from   the   goal
that  this  curriculum  should  develop  students'  sym-
bol  sense.  This  means  developing  "the  ability   to
represent problems in symbolic form and to use   and
interpret  these  symbolic  representations',  and  "the
ability to  identify  the  symbol  manipulations  neces-
sary  to  solve  problems  expressed  in  symbolic  form
and  to  carry  out  manipulations  using  mental   com-
putation,  pencil  and  paper,  a  symbolic  or  graphic
calculator or a computer'.
     It  was  noted  above  that  new  mathematics   cur-
ricula should be designed in  the  expectation  of  fur-
ther  technical  and   scientific   developments.   Most
certainly these will occur  in  artificial  intelligence
and  telecommunir-ations.  In  a  survey   on   Technol-
ogy  and  Mathematics  Education,   James   Fey   [1990]
writes about  artificial  intelligence,  expert  systems
and tutors: "One of the  very  active  areas  of  infor-
matics  research  is  exploring  ways   that   computers
can be  programmed  to  exhibit  'behaviour'  that  sim-
ulates  human  information  processing.  There   are   a
number  of  projects  in  mathematics   education   that
are attempting to  capitalize  on  this  computer  capa-
bility to design programs that  act,  in  various  ways,
like teachers. The most  interesting  work  along  these
lines is producing intelligent tutors for  an  array  of
mathematical  topic  areas  including  arithmetic,   al-
gebra,  geometry  and   proof,   and   calculus.   There
are  some  preliminary  indications  that  those  tutors
provide very  effective  adjuncts  to  regular  teacher-
directed instruction".
     As  for  telecommunications,  one  might  think  that
this will be important for general or  social  education
only. It is likely, however, that the ability to  commu-
nicate  about  mathematical  problems  in  a   worldwide
group  of.peers  will  develop  new  attitudes   towards
problem solving, different  from  the  widespread  "sin-
gle attack" of scientists and  students.  Also,  it  can
be imagined that a feeling for the  benefits  of  inter-
national  and  intercultural  understanding   can   grow
more  intense  through  cooperation   in   a   "serious"
field like mathematics or science, in  addition  to  the
effects of.leisure fields like music, movies, etc.
     We want to  conclude  this  article  by  pointing  to
one of the greatest problems  in  the  changing  of  the
mathematics  curriculum  under  the  challenge  of  com-
puter  systems:  We   must   convince   the   curriculum
makers and those  who  put  changes  into  effect  about
the necessity and the  advantages  of  this  change.  We
hope that this  article  will  provide  good  arguments
to everybody who wants to tackle this problem.
 
 

References

Software
AUTOCALC,   Shell   Centre   for    Mathematical    Edu-
     cation,  University   of   Nottingham   NG7   2RD,
     UK.

CABRI   GEOMtTRk,    Baulac,    Y.,    Bellemain,    F.,
     Laborde,    J.M.,    Laboratoire    L.S.D.    IMAG
     Tour  Irma  BP  53  X,   38041   Grenoble   Cedex,
     1988ff.  MacIntosh,  IBM  PC.  Versions  in  other
     languages such as English  or  German  are  avail-
     able.

DEVELOPING     TRAY,     Inner     London      Education
     Authority,  NCET,  3   Devonshire   Street,   Lon-
     don.

EARLY   SCIENCE    in    Exploring    Primary    Science
     and   Technology   with   Microcomputers,   edited
     by Jan  Stewart,  Council  for  Educational  Tech-
     nology,  NCET,  3   Devonshire   Street,   London.

GEOMETRIC    SUPPOSER,    Schwartz,    J.,     Yerushal-
     my,  M.,  et  al,  Sunburst  Communications   1985
     ff. Apple II, Maclntosh, IBM PC.

GRAPHIX,  Tall,  D.,  van   Blokland,   P.,   Kok,   D.,
     Duisburg:  CoMet   Verlag   far   Unterrichtssoft-
     ware  1989.   ISBN   3-89418-862-6.   IBM-PC.   An
     English version of this program  is  available'for
     example,  through  Sunburst  under  the  title  "A
     Graphic Approach to the Calculus".

KALEIDOSCOPE,   Graf,   K.-D.,   Information   can    be
     obtained from  the  author  at  Freie  Universität
     Berlin, D-W-1000 Berlin 33, Germany.

MODUS,   Walser,    W.,    Wedekind,    J.,    Duisburg:
     CoMet   Verlag   far   Unterrichtssoftware   1992.
     IBM-PC.

SEEK,  Longman,  UK;  also  Shell  Centre   for   Mathe-
     matical  Education,   University   of   Nottingham
     NG72RD,UK.

SYMMETRIC   TURTLES,    Graf,    K.-D.    (see  KALEI-
     DOSCOPE)

TIMES in Teaching  with  a  mz'cro:  Math  3,  Phillips,
     R.      et  al,  1986,  Nottingham:  Shell  Centre  for
     Mathematical Education. BBC Micro.

     Books and Papers

Abelson, H. and  di  Sessa,  A.  [1985]:  Turtle  Geome-
     try:  Computation  as  a  Medium  for   Exploring
     Mathematics, Cambridge: MIT Press.

Biehler,  R.   and   Winkelmann,   B.   [1988]:   Mathe-
     matische   Unterrichissoftware:    BeurteilUngsdi-
     mensz'onen  und  Beispz'ele  in  Schmidt,   Ganter
     (Ed.):       Computer     im     Mathematz'kunterTicht,
     Der  Mathematikunterricht  34,  Heft   4,   19-42.
     ISBN 3-617-24022-4.

Buchberger,  B.  [19901:  Should  Students   Learn   In-
     tegration  Rules,  ACM   SIGSAM   Bulletin,   24,
     1, 10-17.

Dubinsky,  E.  and  Fraser,  R.  [1990]:  Computers  and
     the  Teaching  of  Mathematics,  selected   papers
     from   ICME-6,   Nottingham,   UK:    The    Shell
     Centre for Mathematical Education.

Fey,      J.T.   (1989]:   Technology   and   Education:   A
          Survey  of  Recent  Developments   and   Important
          Problems.   Educational   Studies   in   Mathemat-
          ics, 20, 3, 237-272.

Fey,  J.T.  [1990]:  Technology  and  Mathematics   Edu-
     cation in Dubinsky and Fraser, 73-79.

Fujita, H. and  Terada,  F.  [1991]:  A  Coherent  Study
     of  Mathematics  Education  for  the   Information
     Age; a  Realization  in  the  Japanese  New  Math-
     ematics  Curriculum,  plenary  Lecture  at   ICMI-
     China   Regional   Conference    on    Mathematics
     Education  in  1991,   Beijing,   China.   (Prints
     available from the  first  author,  Department  of
     Mathematics, Meiji University, Japan).

Goldenberg,   E.P.   [1988):   Mathematics,   Metaphors,
     and   Human   Factors:    Mathematical,    Techni-
     cal,  and  Pedagogical  Challenges  in  the   Edu-
     cational  Use  of  Graphical   Representation   of
     Functions,  Journal  of   Mathematical   Behavior,
     7, 2, 135-173.

Graf,  K.-D.  [1988]:  Using  Software  Tools   as   Ad-
     ditional  Tools   in   Geometry   Education   with
Ruler  and  Compasses,   Education   and   Comput-
ing, 4, 3, 171-178.

Graf,  K.-D.  and  Hodgson,  B.   [1990]:   Popularizing
     Geometrical  Concepts:  the  Case  of  the  Kalei-
     doscope, For  the  Learning  of  Mathematics,  10,
     3, 42-50.

Johnson,  D.C.  and  Lovis,  F.  (Eds)  [1987]:   Infor-
     matics  and  the  Teaching  of  Mathematics,  Pro-
     ceedings  of  the  IFIP  TC   3/WG   3.1   Working
     Conference  on  Informatics   and   the   Teaching
     of Mathematics, Sofia,  Bulgaria,  16  -  18  May,
     Amsterdam: North-Holland.

Okamori,   H.   [1989]:   Mathematics   Education    and
     Personal    Computers,     Tokyo:     Daiichi-Hoki
     Shuppan.

Ralston,  A.  [1990]:  A  Framework   for   the   School
     Mathematics  Curriculum  in   2000   in   Dubinsky
     and Fraser [1990], 157-167.

Schumann,  H.  [1990]:  Neue   M6glichkeiten   des   Ge-
     ometrielernens in  der  Planimetrie  durch  inter-
     aktives Konstruieren,  in  Graf,  K.-D.  (Ilrsg.):
     Computer in der Schule 3, Stuttgart: B.  G.
     Teubner, 45-72.

Winkelmann,  B.  [1987]:  Informai:'on  Technology
     Across the Curriculum, in Johnson, D.C.  and
     Lovis, F. (Eds), 89-94.

Winkelmann,  B.   [1992]:   Themenheft   Wachstum.
     Dynamische   Systems   im   Mathemalikunter-
     ticht, Soester Verlagskontor, Soest.